题目内容
【题目】连接三角形各边中点所得的三角形面积与原三角形面积之比为： ．
【答案】1：4
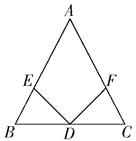
【解析】解：如图所示：
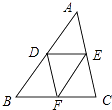
∵D、E、F分别AB、AC、BC的中点，
∴DE、EF、DF是△ABC的中位线，
∴DE= 
BC，EF= AB，DF= AC，
∴ 
= ，
∴△DEF∽△CBA，
∴△DEF的面积：△CBA的面积=（ ）2= 
．
所以答案是：1：4．
【考点精析】本题主要考查了三角形中位线定理和相似三角形的判定与性质的相关知识点，需要掌握连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方才能正确解答此题．
练习册系列答案
相关题目
