题目内容
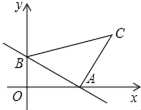
【题目】一次函数y=﹣![]() x+2的图象与x轴,y轴分别交于A、B两点,以AB为腰,作等腰Rt△ABC,则直线BC的解析式为( )
x+2的图象与x轴,y轴分别交于A、B两点,以AB为腰,作等腰Rt△ABC,则直线BC的解析式为( )
A. y=![]() x+2 B. y=﹣
x+2 B. y=﹣![]() x+2 C. y=﹣
x+2 C. y=﹣![]() x+2 D. y=
x+2 D. y=![]() x+2
x+2
【答案】D
【解析】
先根据一次函数的解析式求出A、B两点的坐标,再作CE⊥x轴于点E,由全等三角形的判定定理可得出△ABO≌△CAE,得出C点坐标,用待定系数法即可求出直线BC的解析式;
解:∵一次函数y=﹣![]() x+2中,
x+2中,
令x=0得:y=2;令y=0,解得x=5,
∴B的坐标是(0,2),A的坐标是(5,0).
如图,作CE⊥x轴于点E,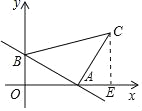
∵∠BAC=90°,
∴∠OAB+∠CAE=90°,
又∵∠CAE+∠ACE=90°,
∴∠ACE=∠BAO.
在△ABO与△CAE中,
![]()
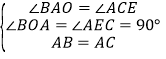 ,
,
∴△ABO≌△CAE(AAS),
∴OB=AE=2,OA=CE=5,
∴OE=OA+AE=2+5=7.
则C的坐标是(7,5).
设直线BC的解析式是y=kx+b,
根据题意得:![]() ,
,
解得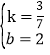 ,
,
∴直线BC的解析式是y=![]() x+2.
x+2.
故选:D.

练习册系列答案
相关题目
【题目】为了解某品牌轿车的耗油情况,将油箱加满后进行了耗油试验,得到如表数据:
轿车行驶的路程s(km) | 0 | 100 | 200 | 300 | 400 | … |
油箱剩余油量Q(L) | 50 | 42 | 34 | 26 | 18 | … |
(1)该轿车油箱的容量为______L,行驶150km时,油箱剩余油量为______L;
(2)根据上表的数据,写出油箱剩余油量Q(L)与轿车行驶的路程s(km)之间的表达式;
(3)某人将油箱加满后,驾驶该轿车从A地前往B地,到达B地时邮箱剩余油量为26L,求A,B两地之间的距离.