题目内容
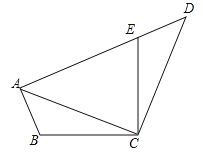
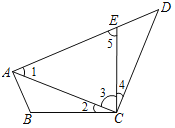
【题目】如图，在△ABC中，∠ACB=90°，点D，E分别是边BC，AB上的中点，连接DE并延长至点F，使EF=2DF，连接CE、AF．
（1）证明：AF=CE；
（2）当∠B=30°时，试判断四边形ACEF的形状并说明理由．
【答案】（1）证明见解析；（2）四边形ACEF是菱形，理由见解析.
【解析】试题分析：（1）由三角形中位线定理得出DE∥AC，AC=2DE，求出EF∥AC，EF=AC，得出四边形ACEF是平行四边形，即可得出AF=CE；
（2）由直角三角形的性质得出∠BAC=60°，AC=
AB=AE，证出△AEC是等边三角形，得出AC=CE，即可得出结论．
试题解析：（1）∵点D，E分别是边BC，AB上的中点，∴DE∥AC，AC=2DE，
∵EF=2DE，∴EF∥AC，EF=AC，∴四边形ACEF是平行四边形，∴AF=CE；
（2）当∠B=30°时，四边形ACEF是菱形；理由如下：
∵∠ACB=90°，∠B=30°，∴∠BAC=60°，AC=
AB=AE，∴△AEC是等边三角形，∴AC=CE，
又∵四边形ACEF是平行四边形，∴四边形ACEF是菱形．
练习册系列答案
相关题目
【题目】永州市是一个降水丰富的地区，今年4月初，某地连续降雨导致该地某水库水位持续上涨，下表是该水库4月1日~4月4日的水位变化情况：
日期x | 1 | 2 | 3 | 4 |
水位y(米) | 20．00 | 20．50 | 21．00 | 21．50 |
(1)请建立该水库水位y与日期x之间的函数模型；
(2)请用求出的函数表达式预测该水库今年4月6日的水位；
(3)你能用求出的函数表达式预测该水库今年12月1日的水位吗？
