Question

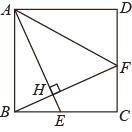
【题目】如图，在矩形ABCD中，AB＝8，AD＝4，点E、F分别在线段AD、AB上，将△AEF沿EF翻折，使得点A落在矩形ABCD内部的P点，连接PD，当△PDE是等边三角形时，BF的长为_____．

Answer 1

【答案】8-2

【解析】

根据等边三角形的性质得到PE=DE，∠DEP=60°，由折叠的性质得到AE=PE，∠AEF=∠PEF=（180°-60°）=60°，根据矩形的性质得到∠A=90°，解直角三角形即可得到结论．

∵△PDE是等边三角形，

∴PE＝DE，∠DEP＝60°，

∵△AEF沿EF翻折，使得点A落在矩形ABCD内部的P点，

∴AE＝PE，∠AEF＝∠PEF＝（180°﹣60°）＝60°，

∴DE＝AE，

∵AD＝4，

∴AE＝2，

∵四边形ABCD是矩形，

∴∠A＝90°，

∴AF＝AE＝2，

∵AB＝8，

∴BF＝AB﹣AF＝8﹣2，

故答案为：8﹣2．