题目内容
【题目】已知:如图,一次函数y=kx﹣1的图象经过点A(3![]() ,m)(m>0),与y轴交于点B.点C在线段AB上,且BC=2AC,过点C作x轴的垂线,垂足为点D.若AC=CD.
,m)(m>0),与y轴交于点B.点C在线段AB上,且BC=2AC,过点C作x轴的垂线,垂足为点D.若AC=CD.
(1)求这个一次函数的表达式;
(2)已知一开口向下、以直线CD为对称轴的抛物线经过点A,它的顶点为P,若过点P且垂直于AP的直线与x轴的交点为Q(﹣![]() ,0),求这条抛物线的函数表达式.
,0),求这条抛物线的函数表达式.

【答案】(1)y=![]() x﹣1;(2)抛物线解析式为:y=
x﹣1;(2)抛物线解析式为:y=![]()
【解析】(1)利用三角形相似和勾股定理构造方程,求AC和m
(2)由∠APQ=90°,构造△PQD∽△APE构造方程求点P坐标可求二次函数解析式.
(1)过点A作AF⊥x轴,过点B作BF⊥CD于H,交AF于点F,过点C作CE⊥AF于点E.
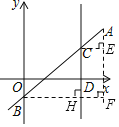
设AC=n,则CD=n
∵点B坐标为(0,-1)
∴CH=n+1,AF=m+1
∵CH∥AF,BC=2AC
∴![]() ,即:
,即:![]()
整理得:
n=![]()
Rt△AEC中,
CE2+AE2=AC2
∴5+(m-n)2=n2
把n=![]() 代入,得:
代入,得:![]()
解得m1=5,m2=-3(舍去)
∴n=3
∴把A(3![]() ,5)代入y=kx-1得
,5)代入y=kx-1得
k=![]()
∴y=![]() x-1
x-1
(2)如图,过点A作AE⊥CD于点E
设点P坐标为(2![]() ,n),由已知n>0
,n),由已知n>0
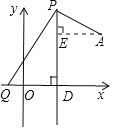
由已知,PD⊥x轴,易证△PQD∽△APE,
∴![]() ,
,
∴![]() ,
,
解得n1=7,n2=-2(舍去).
设抛物线解析式为y=a(x-h)2+k
∴y=a(x-2![]() )2+5
)2+5
把A(3![]() ,5)代入y=a(x-2
,5)代入y=a(x-2![]() )2+7
)2+7
解得a=-![]()
∴抛物线解析式为:y=-![]() x2+
x2+![]() x1
x1

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目