题目内容
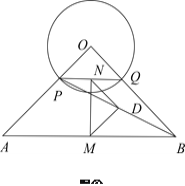
【题目】如图,BC=BD,AD=AE,DE=CE,∠A=36°,则∠B=( )

A. 45B. 36°C. 72°D. 30°
【答案】B
【解析】
由AD=AE,∠A=36°,根据等腰三角形的性质及三角形的内角和定理,即可求得∠ADE的度数;又由三角形外角的性质,即可求得∠CED的度数;由DE=CE,求得∠EDC的度数,然后根据平角的定义求得∠BDC的度数,又由BC=BD,即可求得∠B的值.
∵AD=AE,∠A=36°,
∴∠ADE=∠AED=![]() =72°,
=72°,
∴∠DEC=∠A+∠ADE=36°+72°=108°,
∵DE=CE,
∴∠EDC=∠ECD=![]() =36°,
=36°,
∴∠CDB=180°-∠ADE-∠EDC=72°,
∵BC=BD,
∴∠BCD=∠CDB=72°,
∴∠B=180°-∠BCD-∠CDB=36°.
故选B.

练习册系列答案
相关题目