题目内容
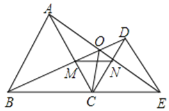
【题目】已知点C在线段BE上,分别以BC、CE为边作等边三角形ABC和等边三角形DCE,连接AE与CD相交于点N,连接BD与AC相交于点M,连接OC、MN,则以下结论①AE=BD;②△ACN≌△BCM;③∠BOE=120°;④△MNC是等边三角形;⑤OC平分∠BOE;正确的个数是( )
A. 2个B. 3个C. 4个D. 5个
【答案】D
【解析】
已知△ABC和△CDE都是等边三角形,根据等边三角形的性质可得CA=CB,CD=CE,∠ACB=60°,∠DCE=60°,即可求得∠ACD=60°,所以∠ACE=∠BCD=120°,再利用SAS即可判定△ACE≌△BCD,由全等三角形的性质可得AE=BD,所以①正确;由△ACE≌△BCD,根据全等三角形的性质可得∠CAE=∠CBD,再利用ASA证明△ACN≌△BCM,由全等三角形的性质可得CN=CM,又因∠MCN=60°,根据有一个角是60°的等腰三角形为等边三角形即可判定△CMN为等边三角形,所以②④正确;由三角形外角的性质可得∠CAE+∠AEC=∠ACB=60°,因为∠CAE=∠CBD,即可得∠CBD+∠AEC=60°,从而求得∠BOE=120°,所以③正确;由△ACE≌△BCD,可得△ACE的面积与△BCD的面积相等,BD=AE,根据三角形的面积公式可得△ACE边AE上的高与△BCD边BD上的高相等,即可得点C到OB、OE的距离相等, 根据角平分线的判定定理可得点C在∠BOE的平分线上,即OC平分∠BOE,所以⑤正确.
∵△ABC和△CDE都是等边三角形,
∴CA=CB,CD=CE,∠ACB=60°,∠DCE=60°,
∴∠ACD=60°,
∴∠ACE=∠BCD=120°,
在△ACE和△BCD中,
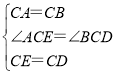 ,
,
∴△ACE≌△BCD(SAS),
∴AE=BD;故①正确;
∵△ACE≌△BCD,
∴∠CAE=∠CBD,
在△ACN和△BCM中,
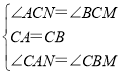 ,
,
∴△ACN≌△BCM(ASA),
∴CN=CM,
而∠MCN=60°,
∴△CMN为等边三角形;故②④正确;
∵∠CAE+∠AEC=∠ACB=60°,
而∠CAE=∠CBD,
∴∠CBD+∠AEC=60°,
∴∠BOE=120°;故③正确;
∵△ACE≌△BCD,
∴△ACE的面积与△BCD的面积相等,
∵BD=AE,
∴△ACE边AE上的高与△BCD边BD上的高相等,
即点C到OB、OE的距离相等,
∴点C在∠BOE的平分线上,
即OC平分∠BOE,故⑤正确.
综上,正确的结论为①②③④⑤,共5个.
故选D.

【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?