题目内容
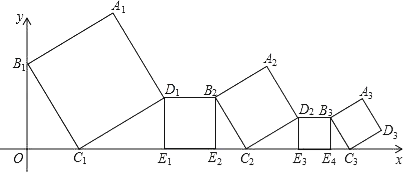
【题目】一组正方形按如图所示放置，其中顶点B1在y轴上，顶点C1，E1，E2，C2，E3，E4，C3…在x轴上．已知正方形A1B1C1D1的边长为1，∠B1C1O＝60°，B1C1∥B2C2∥B3C3，则正方形A2019B2019C2019D2019的边长是_____．
【答案】（
）2018
【解析】
利用正方形的性质结合锐角三角函数关系得出正方形的边长，进而得出变化规律即可得出答案．
解：∵∠B1C1O＝60°，B1C1∥B2C2∥B3C3，
∴∠D1C1E1＝∠C2B2E2＝∠C3B3E4＝30°，
∴D1E1＝C1D1sin30°＝
，
则B2C2＝
，
同理可得：B3C3＝
＝（）2，
故正方形AnBnnDn的边长是：（）n﹣1．
则正方形A2019B2019C2019D2019的边长是：（）2018．
故答案为：（）2018．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
