题目内容
【题目】如图,等边△ABC的边长为2,点D是射线BC上的一个动点,以AD为边向右作等边△ADE,连结CE,
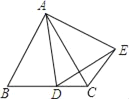
(1)求证:△ABD≌△ACE;
(2)若CE=![]() ,求△ACD的面积;
,求△ACD的面积;
(3)若△ACE是直角三角形,则BD的长是 (直接写出答案).
【答案】(1)见解析;(2)S△ACD=![]() ;(3)1或4.
;(3)1或4.
【解析】
(1)构建两边及其夹角对应相等的两个三角形全等即可证明.
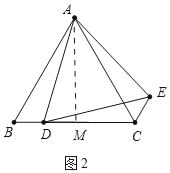
(2)如图2中,作AM⊥BC于M.由(1)可知BD=CE=![]() ,求出CD、AM即可解决问题.
,求出CD、AM即可解决问题.
(3)分两种情形①如图3中,当∠AEC=90°时,②如图4中,当∠CAE=90°时,分别求解即可.
(1)证明:如图1中,
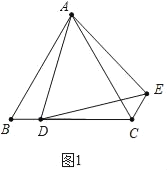
∵△ABC,△ADE是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
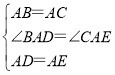 ,
,
∴△BAD≌△CAE.
(2)解:如图2中,作AM⊥BC于M.
∵△ABD≌△ACE,
∴BD=CE=![]() ,∵AB=BC=2,
,∵AB=BC=2,
∴CD=BC﹣BD=![]() ,
,
在Rt△ABM中,∵∠AMB=90°,∠BAM=30°,AB=2,
∴AM=ABcos30=![]() ,
,
∴S△ACD=![]() CDAM=
CDAM=![]() ×
×![]() ×
×![]() =
=![]() .
.
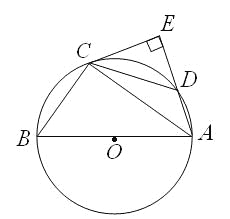
(3)解:如图3中,当∠AEC=90°时,
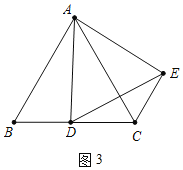
∵△ABD≌△ACE,
∴∠B=∠ACE=60°,
∴∠CAE=90°﹣∠ACE=30°,
∴EC=BD=![]() AC=1.
AC=1.
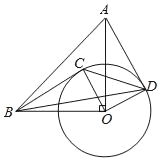
如图4中,当∠CAE=90°时,
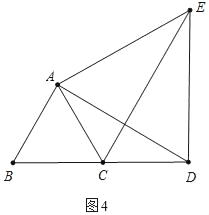
∵△ABD≌△ACE,
∴∠B=∠ACE=60
∴∠CEA=90°﹣∠ACE=30°,
∴EC=2AC=4,
∴BD=CE=4.
综上所述,BD=1或4时,△ACE是直角三角形.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目