题目内容
【题目】如图,△ABC 中,点 D 为边 BC 的点,点 E、F 分别是边 AB、AC 上两点,且 EF∥BC,若 AE:EB=m,BD:DC=n,则( )
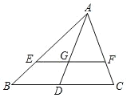
A.若 m>1,n>1,则 2S△AEF>S△ABDB.若 m>1,n<1,则 2S△AEF<S△ABD
C.若 m<1,n<1,则 2S△AEF<S△ABDD.若 m<1,n>1,则 2S△AEF<S△ABD
【答案】D
【解析】
根据相似三角形的判定与性质,得出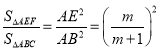 ,
,![]() ,从而建立等式关系,得出
,从而建立等式关系,得出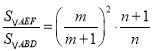 ,然后再逐一分析四个选项,即可得出正确答案 .
,然后再逐一分析四个选项,即可得出正确答案 .
解:∵EF∥BC,若AE:EB=m,BD:DC=n,
∴△AEF∽△ABC,
∴![]() ,
,
∴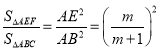 ,
,
∴![]() ,
,
∴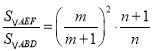
∴当m=1,n=1,即当E为AB中点,D为BC中点时,![]() ,
,
A.当m>1,n>1时,S△AEF与S△ABD同时增大,则![]() 或
或![]() ,即2
,即2![]()
或2![]() >
>![]() ,故A错误;
,故A错误;
B.当m>1,n <1,S△AEF增大而S△ABD减小,则![]() ,即2
,即2![]() ,故B错误;
,故B错误;
C.m<1,n<1,S△AEF与S△ABD同时减小,则![]() 或
或![]() ,即2
,即2![]() 或2
或2![]() <
<![]() ,故C错误;
,故C错误;
D.m<1,n>1,S△AEF减小而S△ABD增大,则![]() ,即2
,即2![]() <
<![]() ,故D正确 .
,故D正确 .
故选D .

练习册系列答案
相关题目