题目内容
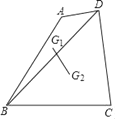
【题目】如图，BD是四边形ABCD的对角线，AB＝BC＝6，∠ABC＝60°，点G1、G2分别是△ABD和△DBC的重心，则点G1、G2间的距离为_____．
【答案】2
【解析】
取BD的中点G，连接AG，CG，AC，根据点G1、G2分别是△ABD和△DBC的重心，得到G1在AG上，G2在CG上，求得
＝
＝
，根据相似三角形的性质得到
＝＝，根据已知条件得到△ABC是等边三角形，求得AC＝6，于是得到结论．
解：取BD的中点G，连接AG，CG，AC，
∵点G1、G2分别是△ABD和△DBC的重心，
∴G1在AG上，G2在CG上，
∴＝＝，
∵∠AGC＝∠AGC，
∴△GG1G2∽△GAC，
∴＝＝，
∵AB＝BC＝6，∠ABC＝60°，
∴△ABC是等边三角形，
∴AC＝6，
∴G1G2＝2，
故答案为：2．
练习册系列答案
相关题目
