题目内容
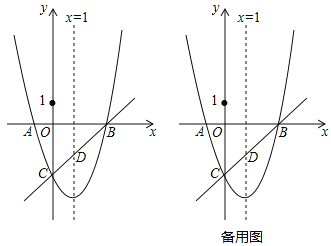
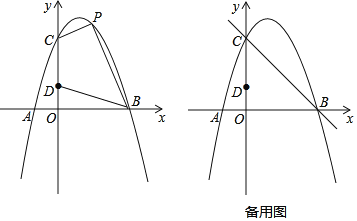
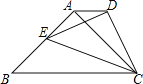
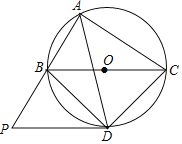
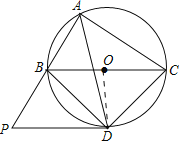
【题目】如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)若AB=3,AC=4,求线段PB的长.
【答案】(1)见解析;(2)PB=![]() .
.
【解析】
(1)由直径所对的圆周角为直角得到∠BAC为直角,再由AD为角平分线,得到一对角相等,根据同弧所对的圆心角等于圆周角的2倍及等量代换确定出∠DOC为直角,与平行线中的一条垂直,与另一条也垂直得到OD与PD垂直,即可得证;
(2)由PD与BC平行,得到一对同位角相等,再由同弧所对的圆周角相等及等量代换得到∠P=∠ACD,根据同角的补角相等得到一对角相等,利用两对角相等的三角形相似;由三角形ABC为直角三角形,利用勾股定理求出BC的长,再由OD垂直平分BC,得到DB=DC,相似三角形的性质,得比例,求出所求即可.
(1)证明:∵圆心O在BC上,
∴BC是圆O的直径,
∴∠BAC=90°,
连接OD,
∵AD平分∠BAC,
∴∠BAC=2∠DAC,
∵∠DOC=2∠DAC,
∴∠DOC=∠BAC=90°,即OD⊥BC,
∵PD∥BC,
∴OD⊥PD,
∵OD为圆O的半径,
∴PD是圆O的切线;
(2)∵PD∥BC,
∴∠P=∠ABC,
∵∠ABC=∠ADC,
∴∠P=∠ADC,
∵∠PBD+∠ABD=180°,∠ACD+∠ABD=180°,
∴∠PBD=∠ACD,
∴△PBD∽△DCA;
∵△ABC为直角三角形,
∴BC2=AB2+AC2=32+42=25,
∴BC=5,
∵OD垂直平分BC,
∴DB=DC,
∵BC为圆O的直径,
∴∠BDC=90°,
在Rt△DBC中,DB2+DC2=BC2,即2DC2=BC2=25,
∴DC=DB=![]() ,
,
∵△PBD∽△DCA,
∴![]() ,
,
则PB=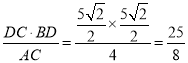 .
.

 阅读快车系列答案
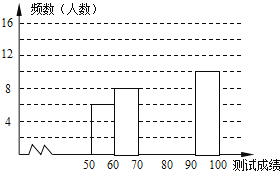
阅读快车系列答案【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数 |
第1组 |
| 6 |
第2组 |
| 8 |
第3组 |
| 14 |
第4组 |
| a |
第5组 |
| 10 |
请结合图表完成下列各题:
![]() 求表中a的值;
求表中a的值; ![]() 频数分布直方图补充完整;
频数分布直方图补充完整;
![]() 若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
![]() 第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.