题目内容
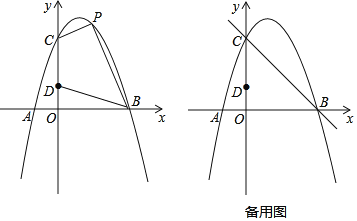
【题目】如图，对称轴为直线x＝1的抛物线经过A（﹣1，0）、C（0，3）两点，与x轴的另一个交点为B，点D在y轴上，且OB＝3OD
（1）求该抛物线的表达式；
（2）设该抛物线上的一个动点P的横坐标为t
①当0＜t＜3时，求四边形CDBP的面积S与t的函数关系式，并求出S的最大值；
②点Q在直线BC上，若以CD为边，点C、D、Q、P为顶点的四边形是平行四边形，请求出所有符合条件的点P的坐标．
【答案】（1）y＝﹣x2+2x+3（2）①t＝
时，S的最大值为
②P（1，4）或（2，3）或（
，
）或（
，）
【解析】
(1)设所求抛物线的表达式为 y＝a(x+1)(x﹣3)，把点C(0，3)代入表达式，即可求解；
(2)①设P(t，﹣t2+2t+3)，则E(t，﹣t+3)，S四边形CDBP＝S△BCD+S△BPC＝
CDOB+PEOB，即可求解；
②分点P在点Q上方、下方两种情况讨论即可求解．
(1)∵抛物线的对称轴为x＝1，A(﹣1，0)，
∴B(3，0)．
∴设所求抛物线的表达式为 y＝a(x+1)(x﹣3)，
把点C(0，3)代入，得3＝a(0+1)(0﹣3)，
解得a＝﹣1，
∴所求抛物线的表达式为y＝﹣(x+1)(x﹣3)，即y＝﹣x2+2x+3；
(2)①连结BC．
∵B(3，0)，C(0，3)，
∴直线BC的表达式为y＝﹣x+3，
∵OB＝3OD，OB＝OC＝3，
∴OD＝1，CD＝2，
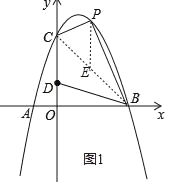
过点P作PE∥y轴，交BC于点E(如图1)．
设P(t，﹣t2+2t+3)，则E(t，﹣t+3)．
∴PE＝﹣t2+2t+3﹣(﹣t+3)＝﹣t2+3t．
S四边形CDBP＝S△BCD+S△BPC＝CDOB+PEOB，
即S＝×2×3+(﹣t2+3t)×3＝﹣(t﹣)2+，
∵a＝﹣＜0，且0＜t＜3，
∴当t＝时，S的最大值为；
②以CD为边，点C、D、Q、P为顶点的四边形是平行四边形，
则PQ∥CD，且PQ＝CD＝2．
∵点P在抛物线上，点Q在直线BC上，
∴点P(t，﹣t2+2t+3)，点Q(t，﹣t+3)．
分两种情况讨论：
(Ⅰ) 如图2，当点P在点Q上方时，
∴(﹣t2+2t+3)﹣(﹣t+3)＝2．即t2﹣3t+2＝0．解得 t1＝1，t2＝2．
∴P1(1，4)，P2(2，3)，
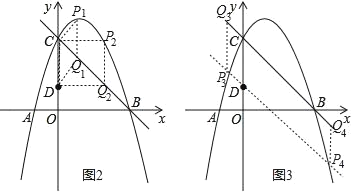
(Ⅱ) 如图3，当点P在点Q下方时，
∴(﹣t+3)﹣(﹣t2+2t+3)＝2．即t2﹣3t﹣2＝0．
解得 t3＝，t4＝，
∴P3(，)，P4(，
)，
综上所述，所有符合条件的点P的坐标分别为：P(1，4)或(2，3)或(，)或(，)．
