题目内容
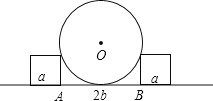
【题目】在汽车车轮修理厂,工人师傅常用两个棱长为a的正方形卡住车轮.如图是其截面图(a小于车轮半径),量出两个正方形的距离AB的长为2b,就可以得出车轮的直径.请你推求出直径d的公式.
【答案】![]()
【解析】
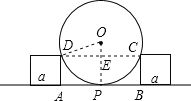
设切点为P,如图,小正方形的顶点分别为C,D,连接CD,OD,OP,OP与CD交于点E,由圆O与AB相切于P,根据切线的性质得到OP与AB垂直,又CD与AB平行,故OP与CD也垂直,根据垂径定理得到E为CD中点,构成直角三角形ODE,设出半径为r,根据DE=AP=b,EP=AD=a,分别表示出DE和OE,在直角三角形ODE中,根据勾股定理列出关于r的方程,求出方程的解即可得到半径r的值,进而求出直径d的值.
如图,设切点为P,小正方形在圆上的顶点分别为C,D,
连接CD,OD,OP,OP与CD交于E,则OP⊥AB,
故OP⊥CD,E为CD中点,设半径为r,
在Rt△ODE中,DE=b,OD=r,OE=r﹣a,
∴根据勾股定理得:(r﹣a)2+b2=r2,
∴r=![]() ,
,
则d=2r=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】铁岭“荷花节”举办了为期15天的“荷花美食”厨艺秀.小张购进一批食材制作特色美食,每盒售价为50元,由于食材需要冷藏保存,导致成本逐日增加,第x天(1≤x≤15且x为整数)时每盒成本为p元,已知p与x之间满足一次函数关系;第3天时,每盒成本为21元;第7天时,每盒成本为25元,每天的销售量为y盒,y与x之间的关系如下表所示:
第x天 | 1≤x≤6 | 6<x≤15 |
每天的销售量y/盒 | 10 | x+6 |
(1)求p与x的函数关系式;
(2)若每天的销售利润为w元,求w与x的函数关系式,并求出第几天时当天的销售利润最大,最大销售利润是多少元?
(3)在“荷花美食”厨艺秀期间,共有多少天小张每天的销售利润不低于325元?请直接写出结果.