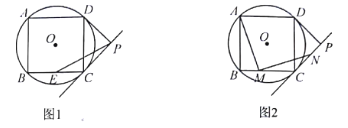
题目内容
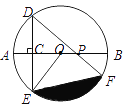
【题目】如图①，直线CD与以线段OB为直径的半⊙A相切于点C，连接OC、BC，作OD⊥CD，垂足为D，OB＝10，
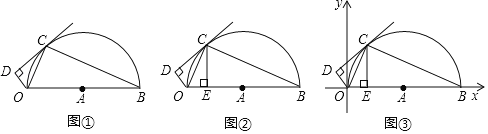
（1）求证：∠OCD＝∠OBC；
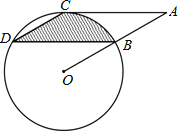
（2）如图②，作CE⊥OB于点E，若CE＝AE，求线段OD的长；
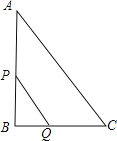
（3）如图③，在（2）的条件下，以O点为原点建立平面直角坐标系求△DOB外接圆的圆心坐标．
以下是优优和乐乐两位同学对第（3）小题的讨论
优优：这题很简单嘛，我只要求出这个三角形任意两条边的中垂线解析式，然后求交点坐标就行了．乐乐：我还有其他的好方法．
如果你是乐乐，你会怎么做？
【答案】（1）证明见解析；（2）5﹣
；（3）△DOB外接圆的圆心坐标为（5，
）
【解析】
（1）连接OC，由题意可得∠OBC＋∠COB＝90°，∠ACO＋∠DCO＝90°，由AC＝OA，可得∠ACO＝∠AOC，即可证∠OCD＝∠OBC；
（2）连接CA，由题意可证△CDO≌△CEO，可得OD＝OE，由OA＝AB＝AC＝5，CE＝AE，CE⊥OB，可得AE＝，即可求OD的长；
（3）设直线CD与x轴交于点N，过点B作BM⊥x轴交直线CD于点M，连接AC，OM，由题意可求∠CAE＝∠ACE＝45°＝∠CNA＝∠CMB，可得AC＝CN，BM＝BN，根据勾股定理可求AN的长，即可求BM的长，可得点M坐标，由∠MDO＝∠MBO＝90°，可证点D，点O，点B，点M四点共圆，即OM是直径，则OM的中点是圆心，也是△DOB外接圆的圆心，根据中点坐标公式可求OM中点坐标．
解：（1）如图：连接OC
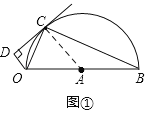
∵OB是直径
∴∠OCB＝90°
∴∠OBC+∠COB＝90°
∵CD是⊙A的切线
∴AC⊥CD
∴∠ACO+∠DCO＝90°
∵AC＝OA
∴∠ACO＝∠AOC
∴∠OCD＝∠OBC；
（2）如图：连接CA
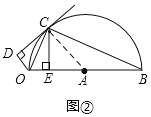
∵CE⊥OB
∴∠COB+∠OCE＝90°且∠OBC+∠COB＝90°
∴∠OCE＝∠OBC且∠OCD＝∠OBC
∴∠OCD＝∠OCE且OC＝OC，∠CDO＝∠CEO＝90°
∴△CDO≌△CEO（AAS）
∴OD＝OE
∵OB＝10，
∴OA＝AB＝AC＝5
∵CE＝AE，CE⊥OB
∴AE2+CE2＝AC2．
∴AE＝＝CE
∴OE＝5﹣＝OD
（3）如图：设直线CD与x轴交于点N，过点B作BM⊥x轴交直线CD于点M，连接AC，OM
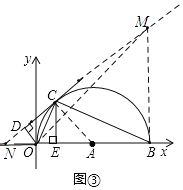
∵CE＝AE，CE⊥OB
∴∠CAE＝∠ACE＝45°，
又∵AC⊥CD
∴∠CNA＝∠CAE＝45°
∴AC＝CN＝5
∴AN＝
＝5
∵BN＝AN+AB
∴BN＝5+5
∵BM⊥AB，∠CNA＝45°
∴∠CNA＝∠CMB＝45°
∴BN＝BM＝5+5，且OB＝10
∴点M的坐标为（10，5+5）
∵∠MDO＝∠MBO＝90°
∴点D，点O，点B，点M四点共圆
∴OM是直径
∴OM的中点是圆心，也是△DOB外接圆的圆心；
∵点O（0，0），点M（10，5+5）
∴△DOB外接圆的圆心坐标为（5，）
