题目内容
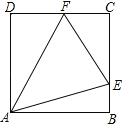
【题目】如图正方形ABCD,E、F分别为BC、CD边上一点.
(1)若∠EAF=45°,求证:EF=BE+DF;
(2)若该正方形ABCD的边长为1,如果△CEF的周长为2.求∠EAF的度数.
【答案】(1)见解析;(2)∠EAF=45°
【解析】
(1)延长CD至E',使DE'=BE,连接AE',先证明△ADE'≌△ABE(SAS),得出∠E′AF=∠EAF,再由SAS证明△E′AF≌△EAF,得出E′F=EF,即可得出结论;
(2)延长CD至E'使DE'=BE,连接AE',可得△ADE'≌△ABE(SAS),然后判断出AE'=AE,∠DAE'=BAE,再求出EF=E'F,进而判断出△E'AF≌△EAF(SSS),得出∠E'AF=∠EAF,即可解决问题.
(1)证明:如图,
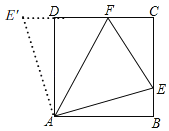
延长CD至E',使DE'=BE,连接AE',
∵四边形ABCD为正方形,
∴AB=AD=CB=CD,∠BAD=∠B=90°,
∴∠ADE'=90°=∠ABE,
在△ADE'和△ABE中,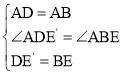 ,
,
∴△ADE'≌△ABE(SAS),
∴AE'=AE,∠DAE'=∠BAE,
∵∠EAF=45°,
∴∠DAF+∠BAE=45°,
∴∠DAF+∠DAE'=∠E'AF=45°=∠EAF,
在△E′AF和△EAF中,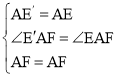 ,
,
∴△E′AF≌△EAF(SAS),
∴E′F=EF,
∵E′F=DE′+DF=BE+DF,
∴EF=BE+DF;
(2)延长CD至E'使DE'=BE,连接AE',
由(1)知,△ADE'≌△ABE(SAS),
∴AE'=AE,∠DAE'=BAE,
设BE=x,DF=y,
∵正方形ABCD的边长为1,
∴CE=1﹣x,CF=1﹣y,
∵△CEF的周长为2,
∴CE+CF+EF=2,
∴1﹣x+1﹣y+EF=2,
∴EF=x+y=BE+DF=DE'+DF=E'F,
在△E'AF和△EAF中, ,
,
∴△E'AF≌△EAF(SSS),
∴∠E'AF=∠EAF,
∴∠DAE'+∠DAF=∠BAE+∠DAF=∠EAF,
∵∠DAF+∠EAF+∠BAE=90°,
∴∠EAF=45°.