题目内容
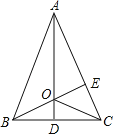
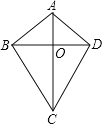
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:①∠ABC=∠ADC;②AC与BD相互平分;③AC,BD分别平分四边形ABCD的两组对角;④四边形ABCD的面积S=![]() ACBD.
ACBD.
(1)写出正确结论的序号;
(2)证明所有正确的结论.
【答案】(1)正确结论是①④;(2)①结论正确;②结论不正确;③结论不正确;④结论正确;证明所有正确的结论见解析.
【解析】
①证明△ABC≌△ADC,可作判断;
②③由于AB与BC不一定相等,则可知此两个选项不一定正确;
④根据面积和求四边形的面积即可.
(1)正确结论是①④,
(2)①在△ABC和△ADC中,
∵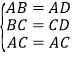 ,
,
∴△ABC≌△ADC(SSS),
∴∠ABC=∠ADC,
故①结论正确;
②∵△ABC≌△ADC,
∴∠BAC=∠DAC,
∵AB=AD,
∴OB=OD,AC⊥BD,
而AB与BC不一定相等,所以AO与OC不一定相等,
故②结论不正确;
③由②可知:AC平分四边形ABCD的∠BAD、∠BCD,
而AB与BC不一定相等,所以BD不一定平分四边形ABCD的对角;
故③结论不正确;
④∵AC⊥BD,
∴四边形ABCD的面积S=S△ABD+S△BCD=![]() BDAO+
BDAO+![]() BDCO=
BDCO=![]() BD(AO+CO)=
BD(AO+CO)=![]() ACBD.
ACBD.
故④结论正确;

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目