题目内容
【题目】如图,A(4,3)是反比例函数y=![]() 在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=
在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=![]() 的图象于点P.
的图象于点P.
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)求点B的坐标;
(3)求△OAP的面积.

【答案】(1)反比例函数解析式为y=![]() ;(2)点B的坐标为(9,3);(3)△OAP的面积=5.
;(2)点B的坐标为(9,3);(3)△OAP的面积=5.
【解析】(1)将点A的坐标代入解析式求解可得;
(2)利用勾股定理求得AB=OA=5,由AB∥x轴即可得点B的坐标;
(3)先根据点B坐标得出OB所在直线解析式,从而求得直线与双曲线交点P的坐标,再利用割补法求解可得.
(1)将点A(4,3)代入y=![]() ,得:k=12,
,得:k=12,
则反比例函数解析式为y=![]() ;
;
(2)如图,过点A作AC⊥x轴于点C,
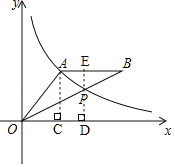
则OC=4、AC=3,
∴OA=![]() =5,
=5,
∵AB∥x轴,且AB=OA=5,
∴点B的坐标为(9,3);
(3)∵点B坐标为(9,3),
∴OB所在直线解析式为y=![]() x,
x,
由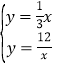 可得点P坐标为(6,2),(负值舍去),
可得点P坐标为(6,2),(负值舍去),
过点P作PD⊥x轴,延长DP交AB于点E,
则点E坐标为(6,3),
∴AE=2、PE=1、PD=2,
则△OAP的面积=![]() ×(2+6)×3﹣
×(2+6)×3﹣![]() ×6×2﹣
×6×2﹣![]() ×2×1=5.
×2×1=5.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】在“元旦”期间,平价商场对该商场商品进行如下的优惠促销活动:
打折前一次性购物总金额 | 优惠措施 |
小于等于 400 元 | 不优惠 |
超过 400 元,但不超过 600元 | 按售价打九折 |
超过 600 元 | 其中 600 元部分八折优惠,超过 600 元的部分打六折优惠 |
按上述优惠条件,若小华一次性购买售价为 80 元/件的商品 n 件时,实际付款 504 元, 则 n=_____.