题目内容
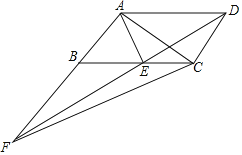
【题目】如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△EAD;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CEF其中正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
由平行四边形的性质得出AD∥BC,AD=BC,由AE平分∠BAD,可得∠BAE=∠DAE,可得∠BAE=∠BEA,得AB=BE,由AB=AE,得到△ABE是等边三角形,②正确;则∠ABE=∠EAD=60°,由SAS证明△ABC≌△EAD,①正确;由△FCD与△ABC等底(AB=CD)等高(AB与CD间的距离相等),得出S△FCD=S△ABC,由△AEC与△DEC同底等高,所以S△AEC=S△DEC,得出S△ABE=S△CEF.④正确;③无法证明得到.
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠EAD=∠AEB,
又∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠BEA,
∴AB=BE,
∵AB=AE,
∴△ABE是等边三角形;
②符合题意;
在△ABC和△EAD中

∴△ABC≌△EAD(SAS);
①符合题意;
∵△FCD与△ABC等底(AB=CD)等高(AB与CD间的距离相等),
∴S△FCD=S△ABC,
又∵△AEC与△DEC同底等高,
∴S△AEC=S△DEC,
∴S△ABE=S△CEF;④符合题意.
若AD与AF相等,即∠AFD=∠ADF=∠DEC
即EC=CD=BE
即BC=2CD,
题中未限定这一条件
∴③不符合题意;
∴①②④符合题意,
故选:B.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
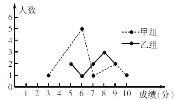
百分学生作业本题练王系列答案【题目】某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀. 为了解本次大赛的成绩,校团委随机抽取了甲、乙两组学生成绩作为样本进行统计,绘制了如下统计图表:
组别 | 平均数 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.8 | a | 3.76 | 90% | 30% |
乙组 | b | 7.5 | 1.96 | 80% | 20% |
(1)求出表中a,b的值;
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面的表格判断,小英属于哪个组?
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组. 但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.