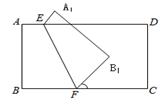
题目内容
在正方形ABCD中,过点A引射线AH,交边CD于点H(点H与点D不重合).通过翻折,使点B落在射线AH上的点G处,折痕AE交BC于E,延长EG交CD于F.
【感知】如图1,当点H与点C重合时,可得FG=FD.

【探究】如图2,当点H为边CD上任意一点时,猜想FG与FD的数量关系,并说明理由.

【应用】在图2中,当AB=5,BE=3时,利用探究结论,求FG的长.
【感知】如图1,当点H与点C重合时,可得FG=FD.

【探究】如图2,当点H为边CD上任意一点时,猜想FG与FD的数量关系,并说明理由.

【应用】在图2中,当AB=5,BE=3时,利用探究结论,求FG的长.
【探究】FG=FD;【应用】 .
.
 .
.试题分析:【探究】连接AF,根据图形猜想FD=FG,由折叠的性质可得AB=AG=AD,再结合AF为△AGF和△ADF的公共边,从而证明△AGF≌△ADF,从而得出结论.
【应用】设FG=x,则FC=5-x,FE=3+x,在RT△ECF中利用勾股定理可求出x的值,进而可得出答案.
【探究】猜想FD=FG.
连接AF,
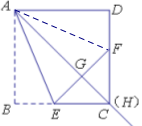
由折叠的性质可得AB=AG=AD,
在Rt△AGF和Rt△ADF中,
 ,
,∴△AGF≌△ADF.
∴FG=FD;
【应用】设GF=
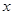 ,则CF=5-
,则CF=5-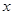 ,则EF=
,则EF=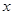 +3
+3在△ECF中由勾股定理得,
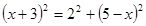 ,解得
,解得
∴FG的长为
 .
.点评:,掌握△AGF≌△ADF始终不变是解答本题的关键,另外在进行结论的应用时,得出Rt△EFC的各边后运用勾股定理进行求解时,要细心避免出错.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目



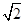 ,则图3中线段
,则图3中线段 的长为 .
的长为 . 
 BFD.
BFD.
 ,正方形ABCD的边长为
,正方形ABCD的边长为 ,猜想
,猜想 的大小,并结合图3证明你的猜想.
的大小,并结合图3证明你的猜想.