题目内容
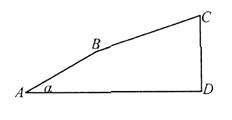
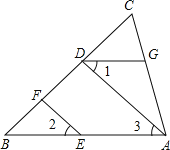
【题目】如图,四边形ABCD中,AD∥BC,DE平分∠ADB,∠BDC=∠BCD.
(1)求证:∠1+∠2=90°;
(2)若∠ABD的平分线与CD的延长线交于F,且∠F=55°,求∠ABC;
(3)若H是BC上一动点,F是BA延长线上一点,FH交BD于M,FG平分∠BFH,交DE于N,交BC于G.当H在BC上运动时(不与B点重合),试判断∠BAD+∠DMH与∠DNG的数量关系,并说明理由.

【答案】(1)证明见解析;(2)70°;(3)∠BAD+∠DMH=2∠DNG,理由见解析
【解析】
(1)由AD∥BC,DE平分∠ADB,得∠ADC+∠BCD=180°,∠BDC=∠BCD,得出∠1+∠2=90°;
(2)由DE平分∠ADB,CD平分∠ABD,四边形ABCD中,AD∥BC,∠F=55°,得出∠ABC=∠ABD+∠DBC=∠ABD+∠ADB,即∠ABC=70°;
(3)在△BMF中,根据角之间的关系∠BMF=180°-∠ABD-∠BFH,得∠GND=180°-∠AED-∠BFG,再根据角之间的关系得∠BAD=∠GND+![]() ∠BFH-∠DBC,再综上得出答案.
∠BFH-∠DBC,再综上得出答案.
(1)∵AD∥BC,
∴∠ADC+∠BCD=180°,
∵DE平分∠ADB,
∴∠BDC=∠BCD,
∴∠ADE=∠EDB,
∠BDC=∠BCD,
∵∠ADC+∠BCD=180°,
∴∠EDB+∠BDC=90°,
∴∠1+∠2=90°;
(2)∵∠FBD+∠BDE=90°﹣∠F=35°,
∵DE平分∠ADB,BF平分∠ABD,
∴∠ADB+∠ABD=2(∠FBD+∠BDE)=70°,
又∵四边形ABCD中,AD∥BC,
∴∠DBC=∠ADB,
∴∠ABC=∠ABD+∠DBC=∠ABD+∠ADB,
即∠ABC=70°;
故答案为:70°
(3)∵在△BMF中,∠BMF=∠DMH=180°﹣∠ABD﹣∠BFH,
又∵∠BAD=180°﹣(∠ABD+∠ADB),
∴∠DMH+∠BAD=(180°﹣∠ABD﹣∠BFH)+(180°﹣∠ABD﹣∠ADB)=360°﹣∠BFH﹣2∠ABD﹣∠ADB,
∴∠DNG=∠FNE=180°﹣![]() ∠BFH﹣∠AED=180°﹣
∠BFH﹣∠AED=180°﹣![]() ∠BFH﹣∠ABD﹣
∠BFH﹣∠ABD﹣![]() ∠ADB=
∠ADB=![]() (∠DMH+∠BAD),
(∠DMH+∠BAD),
即∠BAD+∠DMH=2∠DNG.
故答案为:∠BAD+∠DMH=2∠DNG.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案