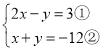题目内容
【题目】如图,AB∥CD.
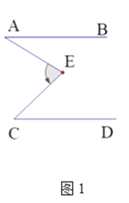
(1)如图1,若∠A=35°,∠C=48°则∠E= °.
(2)如图2,若∠E=120°,∠C=110°,求∠A+∠F的度数;
(3)如图3,若∠E=110°,![]()
![]() ,若GD∥FC,请直接写出∠AGF与∠GDC的数量关系: .
,若GD∥FC,请直接写出∠AGF与∠GDC的数量关系: .


【答案】(1)![]() ;(2)
;(2)![]() ;(3)3∠AGF+∠GDC=220°
;(3)3∠AGF+∠GDC=220°
【解析】
(1)过点E作AB∥EH,根据两直线平行内错角相等,∠A+∠C=∠E即可得出答案;
(2)分别过点E、F作AB∥EH∥FM,内错角相等可得∠A=∠AEH,∠HEF=∠EFM,根据FM∥CD可得∠C+∠MFC=180°即可得出结论;
(3)连接GE并延长,根据外角的性质可得∠E=∠GAE+∠GFE+∠AGF,由(2)中的结论∠A+∠F= =∠E+180°-∠C和![]() 可推出
可推出![]() ,因为GD∥FC可得∠GDC=180°-∠C,进而得出∠AGF与∠GDC的数量关系.
,因为GD∥FC可得∠GDC=180°-∠C,进而得出∠AGF与∠GDC的数量关系.
(1)过点E作AB∥EH,如图,

∵AB∥EH,
∴∠A=∠AEH,
∵AB∥CD,
∴EH∥CD,
∴∠HEC=∠C,
∴∠A+∠C=∠AEH+∠HEC=∠AEC,
∵∠A=35°,∠C=48°,
∴∠AEC=35°+48°=83°,
故答案为:83°;
(2)过点E、F分别作AB∥EH∥FM,如图,

∵AB∥EH∥FM,
∴∠A=∠AEH,∠HEF=∠EFM,
∴∠AEF=∠AEH+∠HEF=∠A+∠EFM,
∵AB∥CD,
∴FM∥CD,
∴∠C+∠MFC=180°,
∴∠MFC=180°-∠C,
∴∠A+∠EFC=∠A+∠EFM+∠MFC=∠AEF+180°-∠C,
∵∠AEF=120°,∠C=110°,
∴∠A+∠EFC =120°+180°-110°=190°;
(3)连接GE并延长,如图,
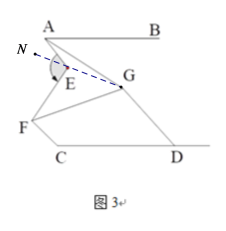
∵∠AEN是△AGE的一个外角,
∴∠AEN=∠GAE+∠AGE,
∵∠FEN是△FGE的一个外角,
∴∠FEN=∠GFE+∠FGE,
∴∠AEF=∠AEN+∠FEN=∠GAE+∠AGE+∠GFE+∠FGE=∠GAE+∠GFE+∠AGF,
∵∠AEF=110°,
∴∠GAE+∠GFE+∠AGF=110°,
∵![]() ,
,
∴![]() ,
,
由(2)得,∠BAE+∠EFC =∠AEF+180°-∠C,
∴![]() ,
,
∴![]() ,
,
∵GD∥FC,
∴∠C+∠GDC=180°,
∴∠GDC=180°-∠C,
∴![]() ,
,
故答案为:![]() .
.

【题目】为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子钟中,各随机抽取10台进行测试,两种电子钟走时误差的数据如下表(单位:秒):
编号 类型 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 |
甲种电子钟 | 1 | -3 | -4 | 4 | 2 | -2 | 2 | -1 | -1 | 2 |
乙种电子钟 | 4 | -3 | -1 | 2 | -2 | 1 | -2 | 2 | -2 | 1 |
(1) 计算甲、乙两种电子钟走时误差的平均数;
(2) 计算甲、乙两种电子钟走时误差的方差;
(3) 根据经验,走时稳定性较好的电子钟质量更优.若两种类型的电子钟价格相同,请问:你买哪种电子钟?为什么?