题目内容
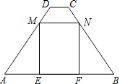
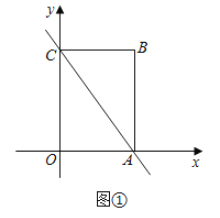
【题目】如图,![]() 是半圆
是半圆![]() 的直径,四边形
的直径,四边形![]() 是内接正方形.
是内接正方形.
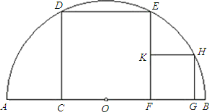
(1)求证:![]() ;
;
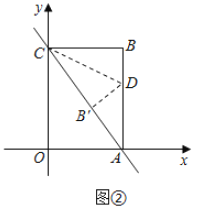
(2)在正方形![]() 的右侧有一正方形
的右侧有一正方形![]() ,点
,点![]() 在
在![]() 上,
上,![]() 在半圆上,
在半圆上,![]() 在
在![]() 上.若正方形
上.若正方形![]() 的边为
的边为![]() ,求正方形
,求正方形![]() 的面积.
的面积.
【答案】(1)详见解析;(2)正方形![]() 的面积为
的面积为![]() .
.
【解析】
(1)连接OD,OE,则OD=OE,求证:OC=OF,可以转化为求证Rt△DOC≌Rt△EOF.
(2)连接OH,在Rt△OEF中勾股定理得到OE,然后在Rt△OHG中根据勾股定理,得到关于设正方形FGHK的边长为x的方程,就可以求出x的值.得到正方形的面积.
(1)证明:连接![]() ,
,![]() ,则
,则![]() ,
,
∵四边形![]() 为正方形
为正方形
∴![]() ,
,![]() ,
,
∴在![]() 和
和![]() 中:
中:
![]() ,
,
∴![]() ,
,
∴![]() .
.
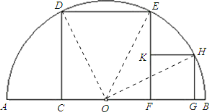
(2)解:连接![]() ,设正方形
,设正方形![]() 的边长为
的边长为![]() .
.
由已知及(1)可得![]() ,
,![]() .
.
在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() .
.
整理得![]() .
.
解得![]() (不合题意,舍去),
(不合题意,舍去),![]() .
.
∴![]()
∴正方形![]() 的面积为
的面积为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目