题目内容
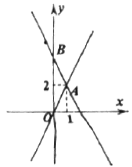
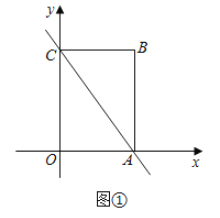
【题目】如图![]() ,已知直线
,已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,以
,以![]() 为边在第一象限内作长方形
为边在第一象限内作长方形![]() .
.
(1)点![]() 的坐标为 ,点
的坐标为 ,点![]() 的坐标为 .
的坐标为 .
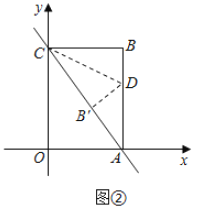
(2)如图![]() ,将△ABC对折,使得点
,将△ABC对折,使得点![]() 与点
与点![]() 重合,折痕
重合,折痕![]() 交
交![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在第一象限内,是否存在点![]() (点
(点![]() 除外),使得
除外),使得![]() 与
与![]() 全等?若存在,请求出点
全等?若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
【答案】(1)(2,0),(2,4);(2)(2,![]() );(3)(
);(3)(![]() ,
,![]() )
)
【解析】
(1)已知直线![]() 与x轴、y轴分别交于点A、C,即可求得A和C的坐标,依据矩形的性质求得点B的坐标;
与x轴、y轴分别交于点A、C,即可求得A和C的坐标,依据矩形的性质求得点B的坐标;
(2)根据题意可知△ACD是等腰三角形,算出AD长即可求得D点坐标;
(3)根据全等三角形的判定方法找出全等三角形,求出符合题意的点P的坐标.
(1)由直线![]() ,
,
令![]() 时,则
时,则![]() ,令
,令![]() 时,则
时,则![]() ,
,
∴点A的坐标为(2,0),点C的坐标为(0,4),
则点B的坐标为(2,4).
故答案是:(2,0),(2,4);
(2)由折叠知:CD=AD.
设AD=![]() ,则CD=
,则CD=![]() ,BD=
,BD=![]() ,
,
根据题意得:![]() ,
,
解得:![]() .
.
此时,AD=![]() ,
,
∴点D的坐标为(2,![]() );
);
(3)当点P在第一象限时,如图,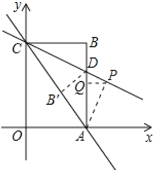
由△APC≌△CBA得∠ACP=∠CAB,
则点P在直线CD上.
过P作PQ⊥AD于点Q,
在Rt△ADP中,![]() ,
,![]() ,
,![]() ,
,
由AD×PQ=DP×AP得:![]() ,
,
∴![]() ,
,
∴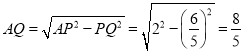 .
.
∴点P的坐标为(![]() ,
,![]() ) .
) .

练习册系列答案
相关题目