题目内容
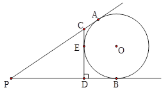
【题目】如图，PA、PB切⊙O于A、B两点，CD切⊙O于点E并垂直PB于D，交PA于C，若⊙O的半径为2，△PCD的周长等于12，则△PCD的面积是（ ）.
A. 6 B. 8 C. 10 D. 12
【答案】A
【解析】
根据切线的性质和勾股定理，可以求得PD、CD的长，从而可以求得△PCD的面积．
连接PO、OA、OC、OE、OB，
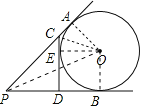
∵PA、PB切⊙O于A、B两点，CD切⊙O于点E并垂直PB于D，
∴PA=PB，CA=CB，DE=DB，OA⊥PA，OB⊥PB，
∴四边形OBDE是正方形，
∵△PCD的周长等于12，
∴PC+CD+PD=12，
∴PC+CA+PD+DB=12，
∴PA=OB=6，
设CA=a，
则PC=6-a，PD=6-2=4，CD=2+a，
∴42+（2+a）2=（6-a）2，
解得，a=1，
∴CD=3，
∴△PCD的面积是：
＝6，
故选A．
练习册系列答案
高效智能课时作业系列答案
相关题目
