题目内容
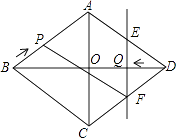
【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG. 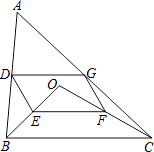
(1)求证:四边形DEFG是平行四边形;
(2)如果∠OBC=45°,∠OCB=30°,OC=4,求EF的长.
【答案】
(1)证明:∵AB、OB、OC、AC的中点分别为D、E、F、G,
∴DG∥BC,DG= ![]() BC,EF∥BC,EF=
BC,EF∥BC,EF= ![]() BC,
BC,
∴DG∥EF,DG=EF,
∴四边形DEFG是平行四边形
(2)解:过点O作OM⊥BC于M,
Rt△OCM中,∠OCM=30°,OC=4
∴OM= ![]() OC=2,
OC=2,
∴CM=2 ![]() ,
,
Rt△OBM中,∠BMO=∠OMB=45°,
∴BM=OM=2,
∴BC=2+2 ![]() ,
,
∴EF=1+ ![]() .
.

【解析】(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得DG∥BC,DG= ![]() BC,EF∥BC,EF=
BC,EF∥BC,EF= ![]() BC,从而得到DG∥EF,DG=EF,然后根据一组对边平行且相等的四边形是平行四边形证明即可;(2)过点O作OM⊥BC于M,由含30°的直角三角形的性质和等腰直角三角形的性质求得结果.
BC,从而得到DG∥EF,DG=EF,然后根据一组对边平行且相等的四边形是平行四边形证明即可;(2)过点O作OM⊥BC于M,由含30°的直角三角形的性质和等腰直角三角形的性质求得结果.
【考点精析】关于本题考查的三角形中位线定理和平行四边形的判定与性质,需要了解连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能得出正确答案.

 计算高手系列答案
计算高手系列答案【题目】某公司生产的某种商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量m(件)与时间t(天)的关系如下表:
时间t(天) | 1 | 3 | 5 | 10 | 36 | … |
日销售量m(件) | 94 | 90 | 86 | 76 | 24 | … |
未来40天内,前20天每天的价格y1(元/件)与时间t(天)的函数关系式为y1= ![]() t+25(1≤t≤20且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系式为y2=﹣
t+25(1≤t≤20且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系式为y2=﹣ ![]() t+40(21≤t≤40且t为整数).
t+40(21≤t≤40且t为整数).
下面我们就来研究销售这种商品的有关问题:
(1)认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m(件)与t(天)之间的表达式;
(2)请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少?