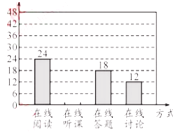
题目内容
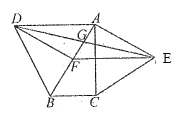
【题目】已知Rt△ABC,∠C=90°,AB=10,且cosA=![]() . M为线段AB的中点, 作DM⊥AB交AC于D. 点Q在线段AC上,点P在线段BC上,以PQ为直径的圆始终过点M, 且PQ交线段DM于点E.
. M为线段AB的中点, 作DM⊥AB交AC于D. 点Q在线段AC上,点P在线段BC上,以PQ为直径的圆始终过点M, 且PQ交线段DM于点E.
⑴ 试说明△AMQ∽△PME;
⑵ 当△PME是等腰三角形时,求出线段AQ的长.
【答案】(1)证明见解析(2)5或![]()
【解析】(1) 连接MC ,根据直角三角形斜边上的中线等于斜边的一半,得到MC=MA=![]() AB,由同弧所对的圆周角相等推出∠A=∠EPM ,再利用同角的余角相等,即可求解; (2)分三种情况讨论:当AM=AQ时; 当QA=QM时; 当MQ=AM时.
AB,由同弧所对的圆周角相等推出∠A=∠EPM ,再利用同角的余角相等,即可求解; (2)分三种情况讨论:当AM=AQ时; 当QA=QM时; 当MQ=AM时.
⑴ 连接MC,
∵∠C=90°,M是AB中点, ∴MC=MA=![]() ,
,
∴∠A=∠MCA,
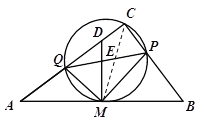
∵∠MCA=∠EPM, ∴∠A=∠EPM.
∵PQ为直径 ,
∴∠PMQ=90°.
∴∠PME+∠QME =90°.
∵DM⊥AB,
∴∠AMD=90°.∴∠AMQ +∠QME =90°.
∴∠AMQ=∠PME,
∴△AMQ∽△PME
⑵AB=10,M为线段AB的中点,∴AM=5,AD=![]() =
=![]() =
=![]()
当△AMQ等腰三角形时,△MPE也是等腰三角形.
当AM=AQ时,AQ=5;
当QA=QM时,AQ=![]() ;
;
由题意MQ≠![]() .
.
综上所述,当△MPE是等腰三角形时,线段AQ长为![]() 或
或![]() .
.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目