题目内容
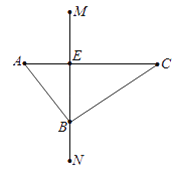
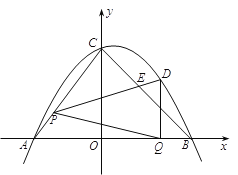
【题目】如图,在平面直角坐标系![]() 中,已知A(-3,0),B(4,0),C(0,4). 二次函数的图像经过A、B、C三点.点P沿AC由点A处向点C运动,同时,点Q沿BO由点B处向点O运动,运动速度均为每秒1个单位长度.当一个点停止运动时,另一个点也随之停止运动.连接PQ,过点Q作QD⊥x轴,与二次函数的图像交于点D,连接PD,PD与BC交于点E. 设点P的运动时间为t秒(t>0).
中,已知A(-3,0),B(4,0),C(0,4). 二次函数的图像经过A、B、C三点.点P沿AC由点A处向点C运动,同时,点Q沿BO由点B处向点O运动,运动速度均为每秒1个单位长度.当一个点停止运动时,另一个点也随之停止运动.连接PQ,过点Q作QD⊥x轴,与二次函数的图像交于点D,连接PD,PD与BC交于点E. 设点P的运动时间为t秒(t>0).
⑴ 求二次函数的表达式;
⑵ 在点P、Q运动的过程中,当∠PQA+∠PDQ=90°时,求t的值;
⑶ 连接PB、BD、CD,试探究在点P,Q运动的过程中,是否存在某一时刻,使得四边形PBDC是平行四边形?若存在,请求出此时t的值与点E的坐标;若不存在,请说明理由.
【答案】⑴![]() ⑵当∠PQA = 90°-∠PDQ时,t的值为
⑵当∠PQA = 90°-∠PDQ时,t的值为![]() ⑶ 不存在某一时刻,使得四边形PBDC是平行四边形
⑶ 不存在某一时刻,使得四边形PBDC是平行四边形
【解析】(1)把A(-3,0),B(4,0),C(0,4)三点代入y=ax+bx+c即可求解;(2)求出直线AC的解析式,利用二次函数的解析式分别设出点P、D的坐标,作PH⊥DQ,可得DQ=2HQ,利用![]() 即可求出t的值;(3)由直线PD与BC相交于E,用含t的代数式设出点E的坐标,点E又在直线BC: y=-x+4上,得到关于t的一元二次方程,再利用根的判别式小于0,判断出方程无解即可.
即可求出t的值;(3)由直线PD与BC相交于E,用含t的代数式设出点E的坐标,点E又在直线BC: y=-x+4上,得到关于t的一元二次方程,再利用根的判别式小于0,判断出方程无解即可.
详解⑴设y=ax+bx+c,把A(-3,0),B(4,0),C(0,4)三点代入得
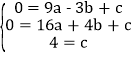 ,解得
,解得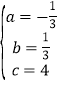
∴![]()
⑵![]() ,
,![]()
作![]() ,
,
∵![]() ∴
∴![]()
∴![]() =
=![]()
解得![]() (舍去),
(舍去),![]() ,
,
∴当∠PQA = 90°-∠PDQ时,![]() 的值为
的值为![]()
⑶不存在某一时刻,使得四边形PBDC是平行四边形.
理由:若四边形PBDC是平行四边形, 则BC平分线段PD,
![]()
∵点E又在直线BC: ![]() 上,
上,
∴![]()
![]()
整理得![]()
此方程根的判别式![]() ,
,
∴方程无实数根.
即不存在某一时刻,四边形PBDC是平行四边形.

 中考解读考点精练系列答案
中考解读考点精练系列答案