ÌâÄżÄÚÈĘ
ĄŸÌâÄżĄż¶šÒćŁșŁšÒ»Ł©ÈçčûÁœžöșŻÊęy1ŁŹy2ŁŹŽæÔÚxÈĄÍŹÒ»žöÖ”ŁŹÊč”Ăy1Łœy2ŁŹÄÇĂŽłÆy1ŁŹy2ÎȘĄ°șÏŚśșŻÊꥱŁŹłÆ¶ÔÓŠx”ÄÖ”ÎȘy1ŁŹy2”ÄĄ°șÏŚś”㥱Ł»Łš¶țŁ©ÈçčûÁœžöșŻÊęÎȘy1ŁŹy2ÎȘĄ°șÏŚśșŻÊꥱŁŹÄÇĂŽy1+y2”ÄŚîŽóÖ”łÆÎȘy1ŁŹy2”ÄĄ°čČÓźÖ”Ą±Łź
Łš1Ł©ĆжÏșŻÊęyŁœ2x+4mÓëyŁœ![]() ÊÇ·ńÎȘĄ°șÏŚśșŻÊꥱŁŹÈçčûÊÇŁŹÇëÇółömŁœ1ʱËüĂǔĥ°șÏŚś”㥱Ł»ÈçčûČ»ÊÇŁŹÇë˔ÜÀíÓÉŁ»
ÊÇ·ńÎȘĄ°șÏŚśșŻÊꥱŁŹÈçčûÊÇŁŹÇëÇółömŁœ1ʱËüĂǔĥ°șÏŚś”㥱Ł»ÈçčûČ»ÊÇŁŹÇë˔ÜÀíÓÉŁ»
Łš2Ł©ĆжÏșŻÊęyŁœ2x+4mÓëyŁœx©1Łš|x|ĄÜ2Ł©ÊÇ·ńÎȘĄ°șÏŚśșŻÊꥱŁŹÈçčûÊÇŁŹÇëÇółöĄ°șÏŚś”㥱Ł»ÈçčûČ»ÊÇŁŹÇë˔ÜÀíÓÉŁ»
Łš3Ł©ÒŃÖȘșŻÊęyŁœx+2mÓëyŁœx2©Łš2m+1Ł©x+Łšm2+4m©3Ł©Łš0ĄÜxĄÜ5Ł©ÊÇĄ°șÏŚśșŻÊꥱŁŹÇÒÓĐΚһĄ°șÏŚś”㥱Łź
ąÙÇółöm”ÄÈĄÖ”·¶Î§Ł»
ąÚÈôËüĂǔĥ°čČÓźÖ”Ą±ÎȘ24ŁŹÊÔÇółöm”ÄÖ”Łź
ĄŸŽđ°žĄżŁš1Ł©ÊÇŁŹxŁœ©3»òxŁœ1Ł»Łš2Ł©Č»ÊÇŁŹŒûœâÎöŁ»Łš3Ł©ąÙ©3ĄÜmŁŒ1»ò2ŁŒmĄÜ6Ł»ąÚmŁœ2©![]() »òmŁœ3Łź
»òmŁœ3Łź
ĄŸœâÎöĄż
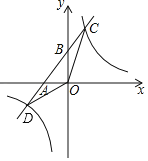
Łš1Ł©ÓÉÓÚ![]() Óë
Óë![]() ¶ŒŸčę”ÚÒ»Ąą”ÚÈęÏóÏȚŁŹËùÒÔÁœžöșŻÊęÓĐč«čȔ㣏żÉÒÔĆжÏÁœžöșŻÊęÊÇĄ°șÏŚśșŻÊꥱŁŹÔÙÁȘÁą
¶ŒŸčę”ÚÒ»Ąą”ÚÈęÏóÏȚŁŹËùÒÔÁœžöșŻÊęÓĐč«čȔ㣏żÉÒÔĆжÏÁœžöșŻÊęÊÇĄ°șÏŚśșŻÊꥱŁŹÔÙÁȘÁą![]() ŁŹœâ”Ă
ŁŹœâ”Ă![]() »ò
»ò![]() ŁŹŒŽżÉÇóĄ°șÏŚś”㥱Ł»
ŁŹŒŽżÉÇóĄ°șÏŚś”㥱Ł»
Łš2Ł©ŒÙÉèÊÇĄ°șÏŚśșŻÊꥱŁŹżÉÇóĄ°șÏŚś”㥱ÎȘ![]() ŁŹÔÙÓÉ
ŁŹÔÙÓÉ![]() ŁŹżÉ”Ă”±
ŁŹżÉ”Ă”±![]() ʱŁŹÊÇĄ°șÏŚśșŻÊꥱŁ»”±
ʱŁŹÊÇĄ°șÏŚśșŻÊꥱŁ»”±![]() »ò
»ò![]() ʱŁŹČ»ÊÇĄ°șÏŚśșŻÊꥱŁ»
ʱŁŹČ»ÊÇĄ°șÏŚśșŻÊꥱŁ»
Łš3Ł©ąÙÓÉÒŃÖȘżÉ”ĂŁș![]() ŁŹœâ”Ă
ŁŹœâ”Ă![]() »ò
»ò![]() ŁŹÔÙÓÉÒŃÖȘżÉ”Ă”±
ŁŹÔÙÓÉÒŃÖȘżÉ”Ă”±![]() ʱŁŹ
ʱŁŹ![]() ŁŹ”±
ŁŹ”±![]() ʱŁŹ
ʱŁŹ![]() ŁŹÒòÎȘÖ»ÓĐÒ»žöĄ°șÏŚś”㥱Ôò
ŁŹÒòÎȘÖ»ÓĐÒ»žöĄ°șÏŚś”㥱Ôò![]() »ò
»ò![]() Ł»ąÚ
Ł»ąÚ![]() ŁŹÓÉąÙżÉ·ÖÁœÖÖÇéżöÇó
ŁŹÓÉąÙżÉ·ÖÁœÖÖÇéżöÇó![]() ”ÄÖ”Łș”±
”ÄÖ”Łș”±![]() ʱŁŹ
ʱŁŹ![]() ʱŁŹ
ʱŁŹ![]() ÔÚ
ÔÚ![]() ”ÄÓĐŚîŽóÖ”ÎȘ
”ÄÓĐŚîŽóÖ”ÎȘ![]() ŁŹ”±
ŁŹ”±![]() ʱŁŹ
ʱŁŹ![]() ʱŁŹ
ʱŁŹ![]() ÔÚ
ÔÚ![]() ”ÄÓĐŚîŽóÖ”ÎȘ
”ÄÓĐŚîŽóÖ”ÎȘ![]() ŁŹ·Ö±đÇółö·ûșÏÌőŒț”Ä
ŁŹ·Ö±đÇółö·ûșÏÌőŒț”Ä![]() Ö”ŒŽżÉŁź
Ö”ŒŽżÉŁź
œâŁșŁš1Ł©![]() ÊÇŸčę”ÚÒ»Ąą”ÚÈęÏóÏȚ”ÄÖ±ÏߣŹ
ÊÇŸčę”ÚÒ»Ąą”ÚÈęÏóÏȚ”ÄÖ±ÏߣŹ![]() ÊÇŸčę”ÚÒ»Ąą”ÚÈęÏóÏȚ”ÄË«ÇúÏߣŹ
ÊÇŸčę”ÚÒ»Ąą”ÚÈęÏóÏȚ”ÄË«ÇúÏߣŹ
![]() ÁœșŻÊęÓĐč«čȔ㣏
ÁœșŻÊęÓĐč«čȔ㣏
![]() ŽæÔÚ
ŽæÔÚ![]() ÈĄÍŹÒ»žöÖ”ŁŹÊč”Ă
ÈĄÍŹÒ»žöÖ”ŁŹÊč”Ă![]() ŁŹ
ŁŹ
![]() șŻÊę
șŻÊę![]() Óë
Óë![]() ÊÇĄ°șÏŚśșŻÊꥱŁ»
ÊÇĄ°șÏŚśșŻÊꥱŁ»
”±![]() ʱŁŹ
ʱŁŹ![]() ŁŹ
ŁŹ
![]() ŁŹœâ”Ă
ŁŹœâ”Ă![]() »ò
»ò![]() ŁŹ
ŁŹ
![]() Ą°șÏŚś”㥱ÎȘ
Ą°șÏŚś”㥱ÎȘ![]() »ò
»ò![]() Ł»
Ł»
Łš2Ł©ŒÙÉèșŻÊę![]() Óë
Óë![]() ÊÇĄ°șÏŚśșŻÊꥱŁŹ
ÊÇĄ°șÏŚśșŻÊꥱŁŹ
![]() ŁŹ
ŁŹ
![]() ŁŹ
ŁŹ
![]() ŁŹ
ŁŹ
![]() ŁŹ
ŁŹ
![]() ŁŹ
ŁŹ
![]() ”±
”±![]() ʱŁŹșŻÊę
ʱŁŹșŻÊę![]() Óë
Óë![]() ÊÇĄ°șÏŚśșŻÊꥱŁ»”±
ÊÇĄ°șÏŚśșŻÊꥱŁ»”±![]() »ò
»ò![]() ʱŁŹșŻÊę
ʱŁŹșŻÊę![]() Óë
Óë![]() Č»ÊÇĄ°șÏŚśșŻÊꥱŁ»
Č»ÊÇĄ°șÏŚśșŻÊꥱŁ»
Łš3Ł©ąÙ![]() șŻÊę
șŻÊę![]() Óë
Óë![]() ÊÇĄ°șÏŚśșŻÊꥱŁŹ
ÊÇĄ°șÏŚśșŻÊꥱŁŹ
![]() ŁŹ
ŁŹ
![]() ŁŹ
ŁŹ
![]() »ò
»ò![]() ŁŹ
ŁŹ
![]() ʱÓĐΚһșÏŚś”㣏
ʱÓĐΚһșÏŚś”㣏
”±![]() ʱŁŹ
ʱŁŹ![]() ŁŹ
ŁŹ
”±![]() ʱŁŹ
ʱŁŹ![]() ŁŹ
ŁŹ
![]() »ò
»ò![]() ʱŁŹÂúŚăÌâÒ⣻
ʱŁŹÂúŚăÌâÒ⣻
ąÚ![]() ŁŹ
ŁŹ
![]() ¶ÔłÆÖáÎȘ
¶ÔłÆÖáÎȘ![]() ŁŹ
ŁŹ
![]() »ò
»ò![]() ŁŹ
ŁŹ
”±![]() ʱŁŹ
ʱŁŹ![]() ʱŁŹ
ʱŁŹ![]() ÔÚ
ÔÚ![]() ”ÄÓĐŚîŽóÖ”ÎȘ
”ÄÓĐŚîŽóÖ”ÎȘ![]() ŁŹ
ŁŹ
![]() ŁŹ
ŁŹ
![]() »ò
»ò![]() ŁŹ
ŁŹ
![]() Ł»
Ł»
”±![]() ʱŁŹ
ʱŁŹ![]() ʱŁŹ
ʱŁŹ![]() ÔÚ
ÔÚ![]() ”ÄÓĐŚîŽóÖ”ÎȘ
”ÄÓĐŚîŽóÖ”ÎȘ![]() ŁŹ
ŁŹ
![]() ŁŹ
ŁŹ
![]() »ò
»ò![]() ŁŹ
ŁŹ
![]() Ł»
Ł»
ŚÛÉÏËùÊöŁș![]() »ò
»ò![]() Łź
Łź

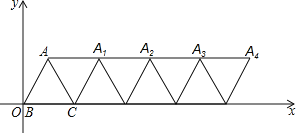
ĄŸÌâÄżĄżÔÚłőÖĐœŚ¶Î”ÄșŻÊęŃ§Ï°ÖĐŁŹÎÒĂÇŸÀúÁËÁĐ±íĄąĂè”㥹ÁŹÏß»șŻÊęÍŒÏóŁŹČąœáșÏÍŒÏóŃĐŸżșŻÊęĐÔÖÊ”ÄčęłÌŁźÒÔÏÂÊÇÎÒĂÇŃĐŸżșŻÊę![]() ĐÔÖÊŒ°ÆäÓŠÓĂ”ÄČż·ÖčęłÌŁŹÇë°ŽÒȘÇóÍêłÉÏÂÁĐžśĐĄÌ⣟
ĐÔÖÊŒ°ÆäÓŠÓĂ”ÄČż·ÖčęłÌŁŹÇë°ŽÒȘÇóÍêłÉÏÂÁĐžśĐĄÌ⣟
Łš1Ł©Çë°ŃϱíČčłäÍêŐûŁŹČąÔÚÍŒÖĐČčÈ«žĂșŻÊęÍŒÏóŁ»
| Ą | Ł5 | Ł4 | Ł3 | Ł2 | Ł1 | 0 | 1 | 2 | 3 | 4 | 5 | Ą |
| Ą |
|
|
| Ł3 | 0 | 3 |
|
|
| Ą |
Łš2Ł©žùŸĘșŻÊęÍŒÏóŁŹĆжÏÏÂÁĐčŰÓÚžĂșŻÊęĐÔÖÊ”ÄË”·šÊÇ·ńŐęÈ·ŁŹŐęÈ·”ÄÔÚÏàÓŠ”ÄÀšșĆÄÚŽòĄ°ĄÌĄ±ŁŹŽíÎó”ÄÔÚÏàÓŠ”ÄÀšșĆÄÚŽòĄ°ĄÁĄ±Ł»
ąÙžĂșŻÊęÍŒÏóÊÇÖá¶ÔłÆÍŒĐÎŁŹËü”ĶԳÆÖáÎȘyÖ᣻( )
ąÚžĂșŻÊęÔÚŚÔ±äÁż”ÄÈĄÖ”·¶Î§ÄÚŁŹÓĐŚîŽóÖ”șÍŚîĐĄÖ”ŁŹ”±![]() ʱŁŹșŻÊęÈĄ”ĂŚîŽóÖ”3Ł»”±
ʱŁŹșŻÊęÈĄ”ĂŚîŽóÖ”3Ł»”±![]() ʱŁŹșŻÊęÈĄ”ĂŚîĐĄÖ”Ł3Ł»( )
ʱŁŹșŻÊęÈĄ”ĂŚîĐĄÖ”Ł3Ł»( )
ąÛ”±![]() »ò
»ò![]() ʱŁŹyËæx”ÄÔöŽó¶űŒőĐĄŁ»”±
ʱŁŹyËæx”ÄÔöŽó¶űŒőĐĄŁ»”±![]() ʱŁŹyËæx”ÄÔöŽó¶űÔöŽóŁ»( )
ʱŁŹyËæx”ÄÔöŽó¶űÔöŽóŁ»( )
Łš3Ł©ÒŃÖȘșŻÊę![]() ”ÄÍŒÏóÈçÍŒËùÊŸŁŹœáșÏÄăËù»”ÄșŻÊęÍŒÏóŁŹÖ±œÓĐŽłöČ»”ÈÊœ
”ÄÍŒÏóÈçÍŒËùÊŸŁŹœáșÏÄăËù»”ÄșŻÊęÍŒÏóŁŹÖ±œÓĐŽłöČ»”ÈÊœ![]() ”ÄœâŒŻŁš±ŁÁô1λХÊ꣏ÎóČîČ»łŹčę0.2Ł©Łź
”ÄœâŒŻŁš±ŁÁô1λХÊ꣏ÎóČîČ»łŹčę0.2Ł©Łź

ĄŸÌâÄżĄżÄłĐŁŚéÖŻÈ«ĐŁŃ§ÉúœűĐĐÁËÒ»ŽÎĄ°Éç»áÖśÒćșËĐÄŒÛÖ”čÛĄ±ÖȘʶŸșÈüŁŹÈüșóËæ»úłéÈĄÁËžśÄêŒ¶Čż·ÖѧÉúłÉŒšœűĐĐÍłŒÆŁŹÖÆŚśÈçÏÂÆ”Êę·ÖČŒ±íșÍÆ”Êę·ÖČŒÖ±·œÍŒŁźÇëžùŸĘÍŒ±íÖĐÌáč©”ÄĐĆÏąŁŹœâŽđÏÂÁĐÎÊÌâŁș
·ÖÊę¶ÎŁš | Æ”Êę | Æ”ÂÊ |
| 4 | 0.1 |
| 8 |
|
|
| 0.3 |
| 10 | 0.25 |
| 6 | 0.15 |
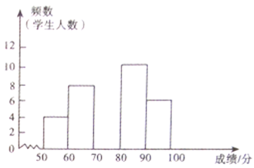
Łš1Ł©ÇëÇółöžĂĐŁËæ»úłéÈĄÁË____ѧÉúłÉŒšœűĐĐÍłŒÆŁ»
Łš2Ł©±íÖĐ![]() ____ŁŹ
____ŁŹ![]() ____ŁŹČąČčÈ«Ö±·œÍŒŁ»
____ŁŹČąČčÈ«Ö±·œÍŒŁ»
Łš3Ł©ÈôÓĂÉÈĐÎÍłŒÆÍŒĂèÊöŽËłÉŒšÍłŒÆ·ÖČŒÇéżöŁŹÔò·ÖÊę¶Î![]() ¶ÔÓŠÉÈĐΔÄÔČĐĜǶÈÊęÊÇ___
¶ÔÓŠÉÈĐΔÄÔČĐĜǶÈÊęÊÇ___![]() Ł»
Ł»
Łš4Ł©ÈôžĂĐŁčČÓĐѧÉú8000ÈËŁŹÇëčÀŒÆžĂĐŁ·ÖÊęÔÚ![]() ”ÄѧÉúÓжàÉÙÈËŁż
”ÄѧÉúÓжàÉÙÈËŁż