题目内容
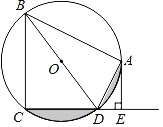
【题目】如图,在距某居民楼AB楼底B点左侧水平距离60m的C点处有一个山坡,山坡CD的坡度(或坡比)![]() ,山坡坡底C点到坡顶D点的距离
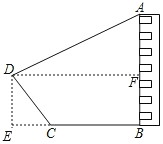
,山坡坡底C点到坡顶D点的距离![]() ,在坡顶D点处测得居民楼楼顶A点的仰角为28°,居民楼AB与山坡CD的剖面在同一平面内,则居民楼AB的高度约为( )
,在坡顶D点处测得居民楼楼顶A点的仰角为28°,居民楼AB与山坡CD的剖面在同一平面内,则居民楼AB的高度约为( )
(参考数据:![]() ,
,![]() ,
,![]() )
)

A.76.9mB.82.1mC.94.8mD.112.6m
【答案】B
【解析】
构造直角三角形,利用坡比的意义和直角三角形的边角关系,分别计算出DE、EC、BE、DF、AF,进而求出AB.
解:如图,由题意得,∠ADF=28°,CD=45,BC=60,
在Rt![]() DEC中,
DEC中,
∵山坡CD的坡度i=1:0.75,
∴![]() =
=![]() =
=![]() ,
,
设DE=4x,则EC=3x,
由勾股定理可得CD=5x,
又CD=45,即5x=45,
∴x=9,
∴EC=3x=27,DE=4x=36=FB,
∴BE=BC+EC=60+27=87=DF,
在Rt![]() ADF中,
ADF中,
AF=tan28°×DF≈0.53×87≈46.11,
∴AB=AF+FB=46.11+36≈82.1,
故选:B.

 名校课堂系列答案
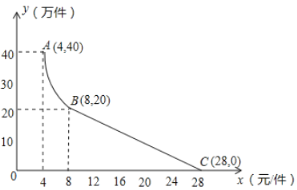
名校课堂系列答案【题目】在初中阶段的函数学习中,我们经历了列表、描点、连线画函数图象,并结合图象研究函数性质的过程.以下是我们研究函数![]() 性质及其应用的部分过程,请按要求完成下列各小题.
性质及其应用的部分过程,请按要求完成下列各小题.
(1)请把下表补充完整,并在图中补全该函数图象;
| … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
| … |
|
|
| -3 | 0 | 3 |
|
|
| … |
(2)根据函数图象,判断下列关于该函数性质的说法是否正确,正确的在相应的括号内打“√”,错误的在相应的括号内打“×”;
①该函数图象是轴对称图形,它的对称轴为y轴;( )
②该函数在自变量的取值范围内,有最大值和最小值,当![]() 时,函数取得最大值3;当
时,函数取得最大值3;当![]() 时,函数取得最小值-3;( )
时,函数取得最小值-3;( )
③当![]() 或
或![]() 时,y随x的增大而减小;当
时,y随x的增大而减小;当![]() 时,y随x的增大而增大;( )
时,y随x的增大而增大;( )
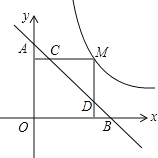
(3)已知函数![]() 的图象如图所示,结合你所画的函数图象,直接写出不等式
的图象如图所示,结合你所画的函数图象,直接写出不等式![]() 的解集(保留1位小数,误差不超过0.2).
的解集(保留1位小数,误差不超过0.2).

【题目】争创全国文明城市,从我做起.尚理中学在八年级开设了文明礼仪校本课程,为了解学生的学习情况,随机抽取了20名学生的测试成绩,分数如下:
94 83 90 86 94 88 96 100 89 82
94 82 84 89 88 93 98 94 93 92
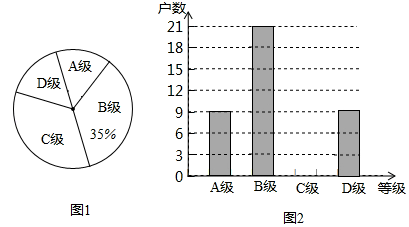
整理上面的数据,得到频数分布表和扇形统计图:
等级 | 成绩/分 | 频数 |
A |
| a |
B |
| 8 |
C |
| 5 |
D |
| 4 |
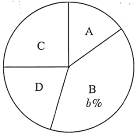
根据以上信息,解答下列问题.
(1)填空:![]() _______,
_______,![]() ______;
______;
(2)若成绩不低于90分为优秀,估计该校1200名八年级学生中,达到优秀等级的人数;
(3)已知A等级中有2名女生,现从A等级中随机抽取2名同学,试用列表或画树状图的方法求出恰好抽到一男一女的概率.