��Ŀ����
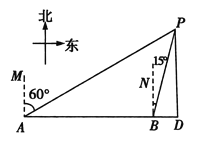
����Ŀ��һ���ִ������������У���A����õ���P��A�ı�ƫ��60��������40���ﵽ��B������ʱ��õ���P��B�ı�ƫ��15������.
(1)�����P���ִ����ߵľ���PD��(�����������)
(2)���ִ���B����������ʱ��һ�ҿ�ͧ�ӵ���P��ͬʱǰ��D�������ܿ�ͧ�ٶ����ִ��ٶȵ�2��������ͧ���DZ��ִ���15���ӵ���D�������ִ�ÿСʱ���ж��ٺ���.(�����ȷ��1����ο�����![]() ��1.7)
��1.7)
���𰸡���1������P���ִ����ߵľ���PD��(10��10![]() )�����2���ִ�ÿСʱԼ����26����.
)�����2���ִ�ÿСʱԼ����26����.
��������
��1������B��BC��AP�ڵ�C�������BC��AC�ij��ȣ�Ȼ��ȷ����CBP�Ķ������̶���ֱ��������PAD�п��������PD��
��2�����ִ�ÿСʱ����x�����Rt��ADP�����AD���̶���ʾ��BD���г����̿ɽ��x��ֵ��
�⣺(1)����B��BC��AP�ڵ�C.
��Rt��ABC����ACB=90������BAC=30����
��BC=![]() AB=20���AC=AB��cos30��=20
AB=20���AC=AB��cos30��=20![]() ����.
����.
�ߡ�PBD=90����15��=75������ABC=90����30��=60����
���CBP=180����75����60��=45����
��PC=BC=20���
��AP=PC��AC=(20��20![]() )����.
)����.
��PD��AD����PAD=30����
��PD=![]() AP=(10��10
AP=(10��10![]() )����.
)����.
��ˣ�����P���ִ����ߵľ���PD��(10��10![]() )����.
)����.
(2)���ִ�ÿСʱ����x���
��Rt��ADP��AD=AP��cos30��=![]() �� (20��20
�� (20��20![]() )=(30��10
)=(30��10![]() )(����)��
)(����)��
��BD=AD��AB=30��10![]() ��40=(10
��40=(10![]() ��10)(����)��
��10)(����)��
�����⣬��![]() ��
��![]() =
=![]() ��
��
���x=60��20![]() ��
��
������x=60��20![]() ��ԭ���̵Ľ⣬
��ԭ���̵Ľ⣬
��x=60��20![]() ��26.
��26.
��ˣ��ִ�ÿСʱԼ����26����.

 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�