题目内容
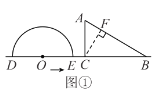
【题目】如图，半圆O的直径DE＝12 cm，在△ABC中，∠ACB＝90°，∠ABC＝30°，BC＝12 cm.半圆O以2 cm/s的速度自左向右运动，在运动过程中，点D，E始终在直线BC上．设运动时间为t s，当t＝0时，半圆O在△ABC的左侧，OC＝8 cm.
(1)当t＝________s时，半圆O与AC所在直线第一次相切；点C到直线AB的距离为________．
(2)当t为何值时，直线AB与半圆O所在的圆相切？
【答案】（1）1，6 cm；（2）当t为4或16时，直线AB与半圆O所在的圆相切．
【解析】
（1）求出路程EC的长，即可以求时间t=1，作C到AB的距离CF，利用直角三角形中30°角所对的直角边是斜边的一半可以得：CF=6；
（2）根据C到AB的距离为6cm，圆的半径为6cm，所以O与C重合，即当O点运动到C点时，半圆O与△ABC的边AB相切，t=8÷2=4秒.
(1)∵DE＝12 cm，
∴OE＝OD＝6 cm.
∵OC＝8 cm，
∴EC＝8－6＝2(cm)，
∴t＝2÷2＝1(s)，
故当t＝1时，半圆O与AC所在直线第一次相切．
如图①，过点C作CF⊥AB于点F.
在Rt△BCF中，∵∠ABC＝30°，BC＝12 cm，
∴CF＝
BC＝6 cm.
故答案为1，6 cm.
(2)如图②，当半圆O在直线AB的左侧，与直线AB相切时，过点O作OM⊥AB于点M，则OM＝6 cm.
∵∠ABC＝30°，
∴OB＝2OM＝12 cm.
又∵BC＝12 cm，
∴当点O与点C重合，即当点O运动到点C时，半圆O与△ABC的边AB相切，此时，点O运动了8 cm，运动时间t＝8÷2＝4.
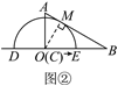
如图③，当半圆O所在的圆在直线AB的右侧与直线AB相切时，设切点为Q，则OQ⊥AB，OQ＝6 cm.
在Rt△QOB中，∠OBQ＝∠ABC＝30°，则OB＝2OQ＝12 cm，此时点O运动了12＋12＋8＝32(cm)，运动时间t＝32÷2＝16.
综上所述，当t为4或16时，直线AB与半圆O所在的圆相切．
