题目内容
【题目】如图,长方形AOBC,以O为坐标原点,OB、OA分别在x轴、y轴上,点A的坐标为(0,8),点B的坐标为(10,0),点E是BC边上一点,把长方形AOBC沿AE翻折后,C点恰好落在x轴上点F处.
(1)求点E、F的坐标;
(2)求AF所在直线的函数关系式;
(3)在x轴上求一点P,使△PAF成为以AF为腰的等腰三角形,请直接写出所有符合条件的点P的坐标.

【答案】(1)(6,0),(10,3);(2)![]() ;(3)(-6,0),(-4,0),(16,0).
;(3)(-6,0),(-4,0),(16,0).
【解析】
(1)易证:ACEAFE,得:AF=AC=10,根据勾股定理,分别求出OF和BE,即可得到答案;
(2)设AF所在直线的函数解析式为:y=kx+b,根据待定系数法,即可求解;
(3)分3种情况:①当AF=AP时,②当AF=PF时,③当AF=PF时,分别求出点P的坐标.
(1)∵长方形AOBC,以O为坐标原点,OB、OA分别在x轴、y轴上,点A的坐标为(0,8),点B的坐标为(10,0),
∴AC=OB=10,BC=OA=8,
∵长方形AOBC沿AE翻折后,C点恰好落在x轴上点F处,
∴ACEAFE,
∴AF=AC=10,
∵在RtAOF中,![]() ,
,
∴![]() ,
,
∴点F坐标是:(6,0),BF=10-6=4,
设BE=x,则FE=CE=8-x,
∵在RtBEF中,![]() ,
,
∴![]() ,解得:x=3,
,解得:x=3,
∴点E的坐标是:(10,3)
(2)设AF所在直线的函数解析式为:y=kx+b,
把A(0,8),F(6,0),代入y=kx+b,得:![]() ,解得:
,解得: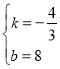
∴AF所在直线的函数解析式为:![]() ;
;
(3)①当AF=AP时,如图1,则OP=OF=6,
∴点P坐标是:(-6,0),
②当AF=PF时,如图2,则PF=10,OP=PF-OF=10-6=4,
∴点P坐标是:(-4,0),
③当AF=PF时,如图3,则PF=10,OP=PF+OF=10+6=16,
∴点P坐标是:(16,0),
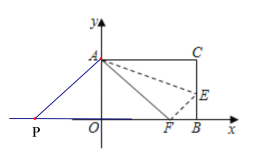

图1 图2

图3







