Question

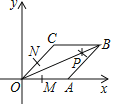
【题目】如图，在平面直角坐标系xOy中，平行四边形OABC的顶点O（0，0），B（3，2），点A在x轴的正半轴上．按以下步骤作图：①以点O为圆心，适当长度为半径作弧分别交边OA、OC于点M、N；②分别以点M、N为圆心，大于MN的长为半径作弧，两弧在∠AOC内交于点P；③作射线OP，恰好过点B，则点A的坐标为（　　）

A.（ ，0）B.（，0）C.（ ，0）D.（2，0）

Answer 1

【答案】A

【解析】

由作法得OB平分∠AOC，利用平行线的性质证明∠ABO＝∠AOB得到AO＝AB，设A（t，0），利用两点间的距离公式得到t2＝（3﹣t）2+22，然后解方程求出t即可得到A点坐标．

解：由作法得OB平分∠AOC，

∴∠AOB＝∠COB，

∵四边形OABC为平行四边形，

∴AB∥OC，

∴∠COB＝∠ABO，

∴∠ABO＝∠AOB，

∴AO＝AB，

设A（t，0），

∴t2＝（3﹣t）2+22，解得t＝，

∴A点坐标为（，0）．

故选：A．