Question

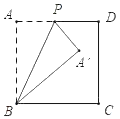
【题目】如图，边长为1的正方形ABCD，点P为边AD上一动点（不与点A重合）．连接BP，将△ABP沿直线BP折叠，点A落在点A′处，如果点A′恰好落在正方形ABCD的对角线上，则AP的长为_____．

Answer 1

【答案】﹣1．

【解析】

根据翻折的性质和正方形的性质以及勾股定理解答即可．

连接A'D，

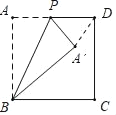
∵将△ABP沿直线BP折叠，点A落在点A′处，如果点A′恰好落在正方形ABCD的对角线上，

∴∠A＝∠PA'B＝∠PA'D＝90°，AP＝A'P，AB＝A'B，

∵边长为1的正方形ABCD，

∴BD＝，

设AP＝x，则PD＝1﹣x，

∴A'P＝AP＝x，DA'＝BD﹣BA'＝BD﹣AB＝﹣1，

在Rt△PDA'中．PD2＝PA'2+A'D2，

即(1-x)2=，

解得：x＝﹣1，

即AP＝﹣1，

故答案为：﹣1．