题目内容
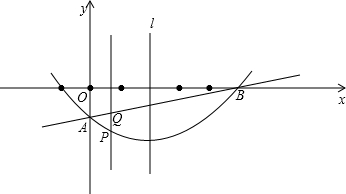
如图,直线y=
x+b经过点B(-
,2),且与x轴交于点A.将抛物线y=
x2沿x轴作左右平移,记平移后的抛物线为C,其顶点为P.
(1)求∠BAO的度数;
(2)直线AB交抛物线y=
x2的右侧于点D,问点B是AD中点吗?试说明理由;
(3)抛物线C与y轴交于点E,与直线AB交于两点,其中一个交点为F.当线段EF∥x轴时,求平移后的抛物线C对应的函数关系式.
| ||
| 3 |
| 3 |
| 1 |
| 3 |
(1)求∠BAO的度数;
(2)直线AB交抛物线y=
| 1 |
| 3 |
(3)抛物线C与y轴交于点E,与直线AB交于两点,其中一个交点为F.当线段EF∥x轴时,求平移后的抛物线C对应的函数关系式.

(1)设直线与y轴交于点M,
将x=-
,y=2代入y=
x+b得b=3,
∴y=
x+3,
当x=0时,y=3,当y=0时x=-3
∴A(-3
,0),M(0,3);
∴OA=3
,OM=3,
∴tan∠BAO=
=
∴∠BAO=30°.
(2)联立直线AB和抛物线的解析式,有:
,解得:
、
∴D(
,
);
已知:A(-3
,0)、B(-
,2),显然点B不是AD的中点.
(3)设抛物线C的解析式为y=
(x-t)2,则P(t,0),E(0,
t2),
∵EF∥x轴且F在抛物线C上,根据抛物线的对称性可知F(2t,
t2),
把x=2t,y=
t2代入y=
x+3
得
t+3=
t2
解得t1=-
,t2=3
∴抛物线C的解析式为y=
(x+
)2或y=
(x-3
)2.

将x=-
| 3 |
| ||
| 3 |
∴y=
| ||
| 3 |
当x=0时,y=3,当y=0时x=-3
| 3 |
∴A(-3
| 3 |
∴OA=3
| 3 |
∴tan∠BAO=
| OM |
| OA |
| ||
| 3 |
∴∠BAO=30°.
(2)联立直线AB和抛物线的解析式,有:
|
|
|
∴D(
| ||||
| 2 |
7+
| ||
| 2 |
已知:A(-3
| 3 |
| 3 |
(3)设抛物线C的解析式为y=
| 1 |
| 3 |
| 1 |
| 3 |
∵EF∥x轴且F在抛物线C上,根据抛物线的对称性可知F(2t,
| 1 |
| 3 |
把x=2t,y=
| 1 |
| 3 |
| ||
| 3 |
得
2
| ||
| 3 |
| 1 |
| 3 |
解得t1=-
| 3 |
| 3 |
∴抛物线C的解析式为y=
| 1 |
| 3 |
| 3 |
| 1 |
| 3 |
| 3 |


练习册系列答案
相关题目