题目内容
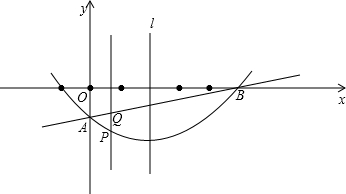
如图,抛物线y=ax2-4ax+c(a≠0)经过A(0,-1),B(5,0)两点,点P是抛物线上的一个动点,且位于直线AB的下方(不与A,B重合),过点P作直线PQ⊥x轴,交AB于点Q,设点P的横坐标为m.
(1)求a,c的值;
(2)设PQ的长为S,求S与m的函数关系式,写出m的取值范围;
(3)以PQ为直径的圆与抛物线的对称轴l有哪些位置关系?并写出对应的m取值范围.(不必写过程)
(1)求a,c的值;
(2)设PQ的长为S,求S与m的函数关系式,写出m的取值范围;
(3)以PQ为直径的圆与抛物线的对称轴l有哪些位置关系?并写出对应的m取值范围.(不必写过程)

(1)∵抛物线y=ax2-4ax+c过A(0,-1),B(5,0)
∴
,
解得:
,
故ac的值分别为
,-1,
抛物线的解析式是y=
x2-
x-1;
(2)∵直线AB经过A(0,-1),B(5,0),
∴直线AB的解析式为y=
x-1,
由(1)知抛物线的解析式为:y=
x2-
x-1,
∵点P的横坐标为m,点P在抛物线上,点Q在直线AB上,PQ⊥x轴,
∴P(m,
m2-
m-1),Q(m,
m-1),
∴S=PQ=(
m-1)-(
m2-
m-1),
即S=-
m2+m(0<m<5);
(3)抛物线的对称轴l为:x=2,
以PQ为直径的圆与抛物线的对称轴l的位置关系有:
相离、相切、相交三种关系,
相离时:|m-2|>
(-
m2+m),
解得0<m<
或
<m<5;
相切时:|m-2|=
(-
m2+m),
解得m=
或m=
;
相交时:|m-2|<
(-
m2+m),
解得
<m<
.
∴
|
解得:
|
故ac的值分别为
| 1 |
| 5 |
抛物线的解析式是y=
| 1 |
| 5 |
| 4 |
| 5 |
(2)∵直线AB经过A(0,-1),B(5,0),
∴直线AB的解析式为y=
| 1 |
| 5 |
由(1)知抛物线的解析式为:y=
| 1 |
| 5 |
| 4 |
| 5 |
∵点P的横坐标为m,点P在抛物线上,点Q在直线AB上,PQ⊥x轴,
∴P(m,
| 1 |
| 5 |
| 4 |
| 5 |
| 1 |
| 5 |
∴S=PQ=(
| 1 |
| 5 |
| 1 |
| 5 |
| 4 |
| 5 |
即S=-
| 1 |
| 5 |
(3)抛物线的对称轴l为:x=2,
以PQ为直径的圆与抛物线的对称轴l的位置关系有:
相离、相切、相交三种关系,
相离时:|m-2|>
| 1 |
| 2 |
| 1 |
| 5 |
解得0<m<
15-
| ||
| 2 |
-5+
| ||
| 2 |
相切时:|m-2|=
| 1 |
| 2 |
| 1 |
| 5 |
解得m=
15-
| ||
| 2 |
-5+
| ||
| 2 |
相交时:|m-2|<
| 1 |
| 2 |
| 1 |
| 5 |
解得
15-
| ||
| 2 |
-5+
| ||
| 2 |

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
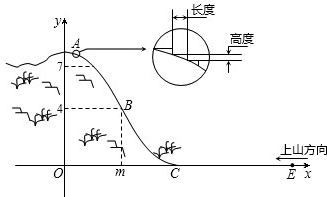 试求索道的最大悬空高度.
试求索道的最大悬空高度.
 ______m2、______m2,在这些数中,x取______m时,面积S最大.
______m2、______m2,在这些数中,x取______m时,面积S最大.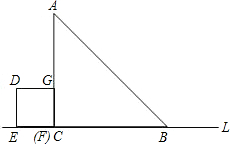 1cm的速度作匀速运动,最后点E与点B重合.
1cm的速度作匀速运动,最后点E与点B重合.