Question

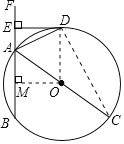
【题目】如图所示，线段AC是⊙O的直径，过A点作直线BF交⊙O于A、B两点，过A点作∠FAC的角平分线交⊙O于D，过D作AF的垂线交AF于E．

（1）证明DE是⊙O的切线；

（2）证明AD2＝2AEOA；

（3）若⊙O的直径为10，DE+AE＝4，求AB．

Answer 1

【答案】（1）证明见解析

（2）证明见解析

（3）8

【解析】

（1）连接OD,由,即可证明

（2）连接CD,根据已知条件证明△ACD∽△ADE即可求解.
（3）过点O作OM⊥AB于点M,则四边形ODEM为矩形,设DE=OM=x则AE＝4﹣x，AM＝5-(4﹣x)＝1+x，在Rt△AMO中，OA2＝AM2+OM2列出方程求解x再利用垂径定理即可求解.

（1）证明：连接OD，

∵

∴

∵AD平分

∴

∴

∴AF∥OD

又∵

∴DE为⊙O切线；

（2）证明：连接CD．

∵AC为⊙O的直径，DE⊥AF

∴∠ADC＝90°，∠DEA＝90°，

∴∠ADC＝∠AED，

∴在△ACD和△ADE中，∠DAC＝∠EAD，∠ADC＝∠AED，

∴△ACD∽△ADE，

∴AD2＝AEAC．

∵AC＝2OA，

∴AD2＝2AEOA；

（3）过点O作OM⊥AB于点M，则四边形ODEM为矩形，设DE＝OM＝x，则AE＝4﹣x，

∴AM＝5﹣（4﹣x）＝1+x，

在Rt△AMO中，OA2＝AM2+OM2，即：（1+x）2+x2＝52

解得：x1＝3，x2＝﹣4（舍去）．

∴AM＝4．

∵OM⊥AB，由垂径定理得：AB＝2AM＝8．