��Ŀ����
����Ŀ������������λ�ڽ������𣬽����忪����䣬�δ����ޣ���Ǭ¡ʮ���꣨1751�꣩�ؽ������ݰ˽ǣ������߶���ԶԶ��ȥ�����ʵĹ�����ӳ����������ƣ�����׳�ۣ�ԭ����ÿ����з���4��8����ƾ��Զ������������������һ�����࣮�����Ϧ������ʱ���ͱ�����������֡������ƽ���������Ե�׳�����ۣ�����Ϊ��������ϼ����ij��ѧ���ۺ���ʵ����С���ͬѧ�ѡ����������������ߡ���Ϊһ������������ƶ��˲��������������ÿ���ʱ�������ʵ�ز�����������������
���� | ���������������� | |||
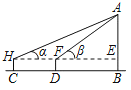
����ʾ��ͼ |
| ˵����ijͬѧ�ڵ�����ѡ���C��ʹ���ֲֳ���ǣ���ô�ʱ¥��A�����ǡ�AHE��������CB����ǰ������D��������C��D֮��ľ���CD��xm���ڵ�Dʹ���ֲֳ���ǣ���ô�ʱ¥��A�����ǡ�AFE���� | ||
�������� | ���Ķ��� | ���Ķ��� | CD�ij��� | ��ͬѧ�۾������ľ���HC |
24�� | 37�� | 32m | 1.76m | |
�� | �� | |||
��1���������С���ͬѧ�����ϱ��еIJ������ݣ�������AB���������ȷ��1m���ο����ݣ�sin24���0.41��cos24���0.91��tan24���0.45��sin37���0.60��cos37���0.80��tan37���0.75��
��2����С��Ҫд��һ�������Ŀ������棬���ϱ��е���Ŀ�⣬����Ϊ����Ҫ������Щ��Ŀ����д��һ�����ɣ�

���𰸡���1��ԼΪ38m����2������Ҫ�������ĿΪ��������̣���Ա�ֹ���ָ����ʦ������ܵȣ����𰸲�Ψһ���������ɣ���
��������
��1����֪�ı���HCDF�Ǿ��Σ��ı���FDBE�Ǿ��Σ�������Ǻ����Ķ������AE��BE�����ɵó��𰸣�
��2����Ҫ���䣺������̣���Ա�ֹ���ָ����ʦ������ܵȣ����𰸲�Ψһ���������ɣ���
�⣺��1����Rt��AFE�У�tan��AFE��![]() ����AFE��37�㣬
����AFE��37�㣬
��![]() ��
��
�ߡ�HCD��90�㣬��FDC��90�㣬
��HC��FD��
�֡�HC��FD��
���ı���HCDF�Ǿ��Σ�
��HF��CD��32m��
��Rt��AHE��tan��AHE��![]() ��
��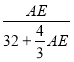 ��0.45��
��0.45��
��ã�AE��36��
ͬ�����ı���FDBE�Ǿ��Σ���BE��FD��HC��1.76m��
��AB��AE+BE��36+1.76=37.76��38��m����
������ABԼΪ38m��
��2������Ҫ�������ĿΪ��������̣���Ա�ֹ���ָ����ʦ������ܵȣ����𰸲�Ψһ���������ɣ���

 ��У����ϵ�д�
��У����ϵ�д�