ЬтФПФкШн
ЁОЬтФПЁПШчЭМ1ЃЌЦНУцжБНЧзјБъЯЕxOyжаЃЌШєAЃЈ0ЃЌ4ЃЉЁЂBЃЈ1ЃЌ0ЃЉЧввдABЮЊжБНЧБпзїЕШбќRtЁїABCЃЌЁЯCABЃН90ЁуЃЌABЃНACЃЎ

ЃЈ1ЃЉШчЭМ1ЃЌЧѓCЕузјБъЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌдкЭМ1жаЙ§CЕузїCDЁЭxжсгкDЃЌСЌНгADЃЌЧѓЁЯADCЕФЖШЪ§ЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЕуAдкyжсЩЯдЫЖЏЃЌвдOAЮЊжБНЧБпзїЕШбќRtЁїOAEЃЌСЌНгECЃЌНЛyжсгкFЃЌЪдЮЪAЕудкдЫЖЏЙ§ГЬжаSЁїAOBЃКSЁїAEFЕФжЕЪЧЗёЛсЗЂЩњБфЛЏЃПШчЙћУЛгаБфЛЏЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉCЃЈ4ЃЌ5ЃЉЃЛЃЈ2ЃЉ45ЁуЃЛЃЈ3ЃЉAЕудкдЫЖЏЙ§ГЬжаSЁїAOBЃКSЁїAEFЕФжЕВЛЛсЗЂЩњБфЛЏЃЌРэгЩМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉЯШХаЖЯЁїAOBЁеЁїCGAЃЌЧѓГіCEЃНOAЃН4ЃЌAGЃНOBЃН1ЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉжЊCЃЈ4ЃЌ5ЃЉЃЌПЩЧѓГіODЃН4ЃЌНјЖјOAЃНODЃЌЕУГіЁЯOADЃН45ЁуЃЌзюКѓгУЦНааЯпЕФаджЪМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЯШХаЖЯЕуEдкyжсЕФзѓВрЃЌдйЗжЕуAдкyжсе§АыжсКЭИКАыжсЩЯЃЌЭЌЃЈ1ЃЉЕФЗНЗЈЧѓГіЕуCзјБъЃЌгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпCEЕФНтЮіЪНЃЌНјЖјЧѓГіЕуFЕФзјБъЃЌМДПЩЕУГіНсТлЃЎ
ЃЈ1ЃЉШчЭМЂйЃЌ
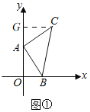
ЁпAЃЈ0ЃЌ4ЃЉЁЂBЃЈ1ЃЌ0ЃЉЃЌ
ЁрOAЃН4ЃЌOBЃН1ЃЌЙ§ЕуCзїCGЁЭyжсгкGЃЌ
ЁрЁЯAGCЃН90ЁуЃНЁЯBOAЃЌ
ЁрЁЯOAB+ЁЯOBAЃН90Ёу
ЁпЁЯCABЃН90ЁуЃЌ
ЁрЁЯOAB+ЁЯGACЃН90ЁуЃЌ
ЁрЁЯOBAЃНЁЯGACЃЌ
ЁпABЃНACЃЌ
ЁрЁїAOBЁеЁїCGAЃЈAASЃЉЃЌ
ЁрCGЃНOAЃН4ЃЌAGЃНOBЃН1ЃЌ
ЁрOGЃНOA+AGЃН5ЃЌ
ЁрCЃЈ4ЃЌ5ЃЉЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉжЊЃЌOAЃН4ЃЌЕуCЃЈ4ЃЌ5ЃЉЃЌ
ЁпCDЁЭxжсЃЌ
ЁрЕуDЃЈ4ЃЌ0ЃЉЃЌ
ЁрODЃН4ЃЌ
ЁрOAЃНODЃЌ
ЁЯOADЃН45ЁуЃЌ
ЁпCDЁЭxжсЃЌ
ЁрCDЁЮyжсЃЌ
ЁрЁЯADCЃНЁЯOADЃН45ЁуЃЛ
ЃЈ3ЃЉAЕудкдЫЖЏЙ§ГЬжаSЁїAOBЃКSЁїAEFЕФжЕВЛЛсЗЂЩњБфЛЏЃЌ
РэгЩЃКЩшЕуAЕФзјБъЮЊЃЈ0ЃЌaЃЉЃЌ
ЂйЕБЕуAдкyжсе§АыжсЩЯЪБЃЌСЌНгCEНЛyжсгкFЃЌ
ЁрЕуCЃЌEдкyжсЕФСНВрЃЌМДЕуEдкyжсзѓВрЃЌ
ЭЌЃЈ1ЃЉЕФЗНЗЈЕУЃЌCЃЈaЃЌa+1ЃЉЃЌ
ЁпЁїOAEЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрAEЁЭOAЃЌ
ЁрEЃЈЉaЃЌaЃЉЃЌ
ЁржБЯпCEЕФНтЮіЪНЮЊyЃН![]() x+a+
x+a+![]() ЃЌ
ЃЌ
ЁрFЃЈ0ЃЌa+![]() ЃЉЃЌ
ЃЉЃЌ
ЁрAFЃНa+![]() -aЃН
-aЃН![]() ЃЌ
ЃЌ
ЁпOBЃН1ЃЌ
Ёр![]() =
=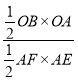 =
=![]() =
=![]() ЃН2ЃЛ
ЃН2ЃЛ
ЂкЕБЕуAдкyжсИКАыжсЩЯЪБЃЌЭЌЂйЕФЗНЗЈЕУЃЌCЃЈЉaЃЌaЉ1ЃЉЃЌEЃЈaЃЌaЃЉЃЌ
ЁржБЯпCEЕФНтЮіЪНЮЊyЃН![]() x+a-
x+a-![]() ЃЌ
ЃЌ
ЁрFЃЈ0ЃЌa-![]() ЃЉЃЌ
ЃЉЃЌ
ЁрAFЃН![]() ЃЌ
ЃЌ
ЁрЁр![]() =
=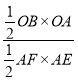 =
=![]() =
=![]() ЃН2ЃЛ
ЃН2ЃЛ
МДAЕудкдЫЖЏЙ§ГЬжаSЁїAOBЁУSЁїAEFЕФжЕВЛЛсЗЂЩњБфЛЏЃЎ

 аТПЮБъЭЌВНбЕСЗЯЕСаД№АИ
аТПЮБъЭЌВНбЕСЗЯЕСаД№АИ