题目内容
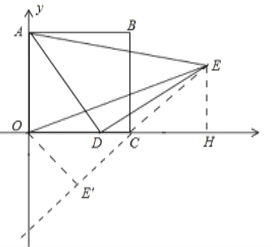
【题目】如图,在平面直角坐标系中,已知正方形 ABCO,边长是 4,点 D(a,0),以 AD 为边在AD 的右侧作等腰 Rt△ADE,∠ADE=90°,连接 OE,则 OE 的最小值为__________________.

【答案】![]()
【解析】
如图,作EH⊥x轴于H,连接CE.利用全等三角形的性质证明∠ECH=45°,推出点E在直线y=x4上运动,作OE′⊥CE,求出OE′的长即可解决问题;
如图,作EH⊥x轴于H,连接CE.
∵∠AOD=∠ADE=∠EHD=90°,
∴∠ADO+∠EDH=90°,∠EDH+∠DEH=90°,
∴∠ADO=∠DEH,
∵AD=DE,
∴△ADO≌△DEH(AAS),
∴OA=DH=OC=4,OD=EH,
∴OD=CH=EH,
∴∠ECH=45°,
故可设CE直线的解析式为y=x+b
把C(4,0)代入得0=4+b
解得b=-4
∴CE直线的解析式为y=x-4
∴点E在直线y=x4上运动,作OE′⊥CE,则△OCE′是等腰直角三角形,
∴CE’=OE’
∵OC=4,
∴CE’2+OE’2=OC2,
即2OE’2=42,
解得OE′=![]() ,
,
∴OE的最小值为![]() .
.
故答案为:![]() .
.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目