题目内容
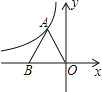
【题目】(![]() 分)如图,在
分)如图,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 在边
在边![]() 上运动,
上运动, ![]() 平分
平分![]() 交边
交边![]() 于点
于点![]() ,
, ![]() 垂足为
垂足为![]() ,
, ![]() 垂足为
垂足为![]() .
.


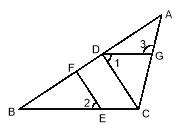
(![]() )当
)当![]() 时,求证:
时,求证: ![]() .
.
(![]() )探究:
)探究: ![]() 为何值时,
为何值时, ![]() 与
与![]() 相似?
相似?
(![]() )直接写出:
)直接写出: ![]() __________时,四边形
__________时,四边形![]() 与
与![]() 的面积相等.
的面积相等.
【答案】(1)见解析;(2)5或![]() ;(3)
;(3)![]()
【解析】试题分析:似三角形的判定得出△DEB∽△ACB,从而得出角的关系,再由AD=CD,得出BD与AB的关系,即可求的结论.
(2)此题分两种情况求解,△BME∽△CNE或△BME∽△ENC,根据相似三角形的性质即可求得;
(3)根据四边形的面积求解方法,利用分割法求不规则四边形的面积,作辅助线EN⊥BD即可求得
解:(![]() )∵
)∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() 是
是![]() 的平分线,
的平分线,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(![]() )(i)当
)(i)当![]() 时,得
时,得![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
, ![]() ,
,
又![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() .
.
(ii)当![]() 时,得
时,得![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() 即
即![]() 是
是![]() 斜边上的高,
斜边上的高,
由三角形面积公式得![]() ,
,
∴![]() ,
,
∴![]() ,
,
综上,当![]() 或
或![]() 时,
时, ![]() 与
与![]() 相似.
相似.
(![]() )
)![]() ,
,
由角平分线性质易得![]() ,
,
∵![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() 是
是![]() 的垂直平分线,
的垂直平分线,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,①
,①
∴![]() 即
即![]() ,
,
∵![]() ,
,
∴![]() ,
,
由①得![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目
【题目】某公交车每天的支出费用为600元每天的乘车人数x(人)与每天利润(利润=票款收入-支出费用)y(元)的变化关系如下表所示(每位乘客的乘车票价固定不变): 根据表格中的数据,回答下列问题:
x(人) | …… | 200 | 250 | 300 | 350 | 400 | …… |
y(元) | …… | -200 | -100 | 0 | 100 | 200 | …… |
(1)在这个变化关系中,自变量是什么?因变量是什么?
(2)若要不亏本,该公交车每天乘客人数至少达到多少?
(3)请你判断一天乘客人数为500人时利润是多少?
(4)试写出该公交车每天利润y(元)与每天乘车人数x(人)的关系式.