题目内容
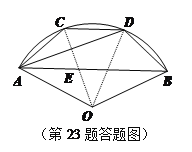
【题目】如图,点A,C,D,B在以O点为圆心,OA长为半径的圆弧上, AC=CD=DB,AB交OC于点E.求证:AE=CD.

【答案】证明见解析
【解析】试题分析:连接OC,OD,根据弦相等,得出它们所对的弧相等,得到![]() =
=![]() ,再得到它们所对的圆心角相等,证明
,再得到它们所对的圆心角相等,证明![]() 得到
得到![]()
又因为![]() 即可证明.
即可证明.
试题解析:证明:方法一:连接OC,OD,
∵AC=CD=DB, ![]() =
=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() .
.
方法二:连接OC,OD,
∵AC=CD=DB, ![]() =
=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵∠CAO=∠CAE+∠EAO,∠AEC=∠AOC+∠EAO,
∴∠CAO=∠AEC,
在![]() 中,
中, ![]()
∴∠ACO=∠CAO,
∴∠ACO=∠AEC, ![]() ,
,
![]() ,
, ![]() .
.
方法三:连接AD,OC,OD,
∵AC=DB, ![]() =
=![]() ,
,
∴∠ADC=∠DAB,
∴CD∥AB,
∴∠AEC=∠DCO,
∵AC=CD,AO=DO,
∴CO⊥AD,
∴∠ACO=∠DCO,
∴∠ACO=∠AEC,∴AC=AE,
∵AC=CD,∴AE=CD.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目