题目内容
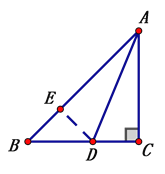
【题目】(1)如图1,在△ABC中,∠ACB=2∠B,∠C=90°,AD为∠BAC的平分线交BC于D,求证:AB=AC+CD.(提示:在AB上截取AE=AC,连接DE)



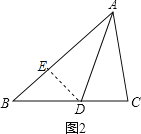
(2)如图2,当∠C≠90°时,其他条件不变,线段AB、AC、CD又有怎样的数量关系,直接写出结果,不需要证明.
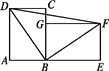
(3)如图3,当∠ACB≠90°,∠ACB=2∠B ,AD为△ABC的外角∠CAF的平分线,交BC的延长线于点D,则线段 AB、AC、CD又有怎样的数量关系?写出你的猜想,并加以证明.
【答案】(1)见解析;(2)AB=AC+CD;(3)AB=CD﹣AC
【解析】试题分析:(1)在AB上截取AE=AC,连接DE,根据角平分线的定义得到∠1=∠2.推出△ACD≌△AED(SAS).根据全等三角形的性质得到∠AED=∠C=90,CD=ED,根据已知条件得到∠B=45°.求得∠EDB=∠B=45°.得到DE=BE,等量代换得到CD=BE.即可得到结论;
(2)在AC取一点E使AB=AE,连接DE,易证△ABD≌△AED,所以∠B=∠AED,BD=DE,又因为∠B=2∠C,所以∠AED=2∠C,因为∠AED是△EDC的外角,所以∠EDC=∠C,所以ED=EC,BD=EC,进而可证明AB+BD=AE+EC=AC;
(3)在AB的延长线AF上取一点E,使得AE=AC,连接DE.证明△ACD≌△AED,根据全等三角形的性质得到DE=BE,BE=CD,即可得出结论.
试题解析:(1)证明:在AB上取一点E,使AE=AC
∵AD为∠BAC的平分线
∴∠BAD=∠CAD.
在△ACD和△AED中,
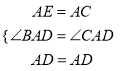
∴△ACD≌△AED(SAS).
∴∠AED=∠C=90°,CD=ED,
又∵∠ACB=2∠B,∠C=90°,
∴∠B=45°. ∴∠EDB=∠B=45°.
∴DE=BE, ∴CD=BE.
∵AB=AE+BE, ∴AB=AC+CD.
(2)证明:在AB取一点E使AC=AE,
在△ACD和△AED中,
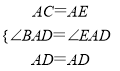 ,
,
∴△ACD≌△AED,
∴∠C=∠AED,CD=DE,
又∵∠C=2∠B,
∴∠AED=2∠B,
∵∠AED是△EDC的外角,
∴∠EDB=∠B,
∴ED=EB,
∴CD=EB,
∴AB=AC+CD;
(3)猜想:AB=CD﹣AC
证明:在BA的延长线上取一点E,使得AE=AC,连接DE,
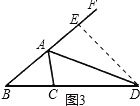
在△ACD和△AED中,
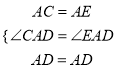 ,
,
∴△ACD≌△AED(SAS),
∴∠ACD=∠AED,CD=DE,
∴∠ACB=∠FED,
又∵∠ACB=2∠B
∴∠FED=2∠B,
又∵∠FED=∠B+∠EDB,
∴∠EDB=∠B,
∴DE=BE,
∴BE=CD,
∵AB=BE-AE
∴AB=CD﹣AC.

 阅读快车系列答案
阅读快车系列答案