题目内容
【题目】如图,把长方形ABCD旋转到长方形GBEF的位置,此时点A,B,E在一条直线上.
(1)指出这个过程中的旋转中心,并说明旋转角度数是多少;
(2)指出图中的对应线段;
(3)连接BD,BF,DF,判断△DBF的形状,并说明理由.
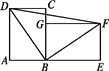
【答案】(1)旋转中心为点B,旋转角度数是90°;(2)对应线段:AB与GB,AD与GF,DC与FE,BC与BE;(3)△DBF是等腰直角三角形,理由见解析.
【解析】试题分析:(1)由长方形的性质得出∠ABC=90°,由已知条件和旋转的性质得出∠CBE=180°-90°=90°,得出旋转中心是点B,旋转角度数是90°;
(2)由旋转的性质得出长方形GBEF≌长方形ABCD,得出BG=BA,BE=BC,EF=CD,GF=AD,即可得出结果;
(3)由旋转的性质得:BF=BD,∠DBF=∠CBE=90°,即可得出结论.
试题解析:(1)∵四边形ABCD是长方形,
∴∠ABC=90°,
∵把长方形ABCD旋转到长方形GBEF的位置,此时点A,B,E在一条直线上,
∴∠CBE=180°-90°=90°,
∴旋转中心是点B,旋转角度数是90°;
(2)由旋转的性质得:长方形GBEF≌长方形ABCD,
∴BG=BA,BE=BC,EF=CD,GF=AD,BF=BD,
∴图中的对应线段为BG和BA,BE和BC,EF和CD,GF和AD,BF和BD;
(3)△DBF是等腰直角三角形;理由如下:
由旋转的性质得:BF=BD,∠DBF=∠CBE=90°,
∴△DBF是等腰直角三角形.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目