��Ŀ����
����Ŀ�����꼶�߰ࡰ��ѧ��ȤС�顱�Ժ����ĶԳƱ任����̽����������̽���������ù��̣��벹��������
��1���������֣���������y=|x|��ͼ��ʱ�������˷ֶκ����İ취���ú���ת��Ϊy= ![]() ��������ͼ1��ʾ��ƽ��ֱ������ϵ������������ͼ��
��������ͼ1��ʾ��ƽ��ֱ������ϵ������������ͼ��
��2�����̽��
������y=|x��1|��ͼ����ת��Ϊ�ֶκ��� �� Ȼ��ֱ��������κ�����ͼ������С꿣���������ƽ���ϵ���Գ�֪ʶ���Ѻ���y=x��1��x�����沿�֣���x����з��ۣ���x���ϼ����沿������˺���y=|x��1|��ͼ����ͼ��ʾ��
��3����չ���
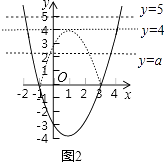
��ͼ2��ͼ�Ǻ���y=x2��2x��3��ͼ������ԭ����ϵ������y=|x2��2x��3|��ͼ��
��4��ʵ������
�ٺ��� ![]() ��ͼ����x���������㣬��Ӧ����|x2��2x��3|=0����ʵ����
��ͼ����x���������㣬��Ӧ����|x2��2x��3|=0����ʵ����
�ں��� ![]() ��ͼ����ֱ��y=5�������㣬��Ӧ����|x2��2x��3|=5����ʵ����
��ͼ����ֱ��y=5�������㣬��Ӧ����|x2��2x��3|=5����ʵ����
�ۺ��� ![]() ��ͼ����ֱ��y=4�������㣬��Ӧ����
��ͼ����ֱ��y=4�������㣬��Ӧ���� ![]() ����ʵ����
����ʵ����
�ܹ���x�ķ��� ![]() ��4��ʵ��ʱ��a��ȡֵ��Χ�� ��
��4��ʵ��ʱ��a��ȡֵ��Χ�� ��
���𰸡�
��1��
�⣺��ͼ1��
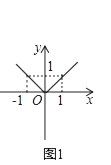
��2��![]()
��3��
�⣺�Ѻ���y=x2��2x��3��ͼ����x�����沿�֣���x����з��ۣ���x���ϼ����沿������˺���y=|x2��2x��3|��ͼ����ͼ2��
��4��2��2��2��2��3��3��0��a��4
���������⣺��2.�����̽��
������y=|x��1|��ͼ����ת��Ϊ�ֶκ���y= ![]() ����4��ʵ�����âٺ���y=|x2��2x��3|��ͼ����x���� 2�����㣬��Ӧ����|x2��2x��3|=0��2��ʵ�����ں���y=|x2��2x��3|��ͼ����ֱ��y=5�� 2�����㣬��Ӧ����|x2��2x��3|=5��2��ʵ�����ۺ���y=|x2��2x��3|��ͼ����ֱ��y=4��3�����㣬��Ӧ����|x2��2x��3|=4��3��ʵ�����ܹ���x�ķ���|x2��2x��3|=a��4��ʵ��ʱ��a��ȡֵ��Χ�� 0��a��4��
����4��ʵ�����âٺ���y=|x2��2x��3|��ͼ����x���� 2�����㣬��Ӧ����|x2��2x��3|=0��2��ʵ�����ں���y=|x2��2x��3|��ͼ����ֱ��y=5�� 2�����㣬��Ӧ����|x2��2x��3|=5��2��ʵ�����ۺ���y=|x2��2x��3|��ͼ����ֱ��y=4��3�����㣬��Ӧ����|x2��2x��3|=4��3��ʵ�����ܹ���x�ķ���|x2��2x��3|=a��4��ʵ��ʱ��a��ȡֵ��Χ�� 0��a��4��
�ʴ�Ϊy= ![]() ��2��2��2��2��3��3��0��a��4��
��2��2��2��2��3��3��0��a��4��
��1��������㷨��y=|x|��ͼ��2�����ݾ���ֵ�����壬���÷������۵�˼��д���ֶκ�������3���루2��������ͼ��ķ���һ�����Ѻ���y=x2��2x��3��ͼ����x�����沿�֣���x����з��ۿɵõ�����y=|x2��2x��3|��ͼ��4�����û�����ͼ��ͨ��ȷ��y=|x2��2x��3|��ͼ����ֱ��y=a�Ľ������������⣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��ij������ʦ���Լ��ν̵�55����������һ�������ײ��ԣ����涨�����ɼ�Ϊ16��ϸ��±��������ȡ��10��������A��B������Եijɼ���ϸ���IJ�ֵ���Ⱥϸ���������Ϊ�����ٵ�����Ϊ������
A �� | -1.5 | +1.5 | -1 | -2 | -2 |
B�� | +1 | +3 | -3 | +2 | -3 |
��1����������55�������кϸ��������Լ�Ƕ��٣�
��2��ͨ����صļ��㣬˵���ĸ���ijɼ��ȽϾ��ȣ�
��3�����پٳ���������˵��A��ɼ�����B��ɼ������ҳ�һ��������˵��B�����A�顣