题目内容
如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( ).


| A.4cm | B.5cm |
| C.6cm | D.10cm |
B.
试题分析:先根据勾股定理求出AB的长,再由图形折叠的性质可知,AE=BE,故可得出结论:
∵△ABC是直角三角形,两直角边AC=6cm、BC=8cm,
∴
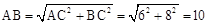 (cm).
(cm).∵△ADE由△BDE折叠而成,∴AE=BE=
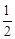 AB=
AB=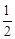 ×10=5(cm).
×10=5(cm).故选B.
考点: 1.翻折变换(折叠问题);2.勾股定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
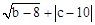 =0,则三角形的形状是( )
=0,则三角形的形状是( )