题目内容
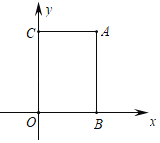
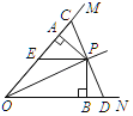
【题目】如图平面直角坐标系中,A点坐标为(0,1),AB=BC=![]() ,∠ABC=90°,CD⊥x轴.
,∠ABC=90°,CD⊥x轴.
(1)填空:B点坐标为 ,C点坐标为 .
(2)若点P是直线CD上第一象限上一点且△PAB的面积为6.5,求P点的坐标;
(3)在(2)的条件下点M是x轴上线段OD之间的一动点,当△PAM为等腰三角形时,直接写出点M的坐标.

【答案】(1)(3,0),(4,3);(2)P(4,4);(3)(1,0)或(![]() ).
).
【解析】
(1)根据勾股定理可求出OB=3,证明△AOB≌△DBC,可得出OA=BD=1,OB=DC=3,则B,C两点的坐标可求出;
(2)设P(4,a),由三角形面积可得出关于a的方程,解方程即可得出答案;
(3)根据M是x轴上线段OD之间的一动点,画出图形,有两种可能,当AP=MP或AM=MP时,设M(x,0),可得出关于x的方程,解方程即可得解.
解:(1)∵A点坐标为(0,1),AB=BC=![]() ,
,
∴OB=![]() =
=![]() =3,
=3,
∵∠ABC=90°,∠AOB=90°,
∴∠OAB+∠ABO=90°,∠ABO+∠CBD=90°,
∴∠OAB=∠CBD,
∵∠AOB=∠BDC,
∴△AOB≌△DBC(AAS),
∴OA=BD=1,OB=DC=3,
∴B(3,0),C(4,3),
故答案为:(3,0),(4,3);
(2)如图1,设P(4,a),
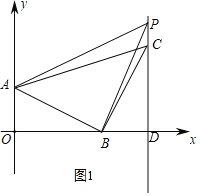
∵△PAB的面积为6.5,
∴S△PAB=S四边形AODP﹣S△AOB﹣S△BDP=![]() =6.5,
=6.5,
解得:a=4,
∴P(4,4);
(3)M是x轴上线段OD之间的一动点,如图2,当AP=MP,
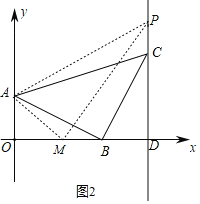
∵P(4,4),A(0,1),设M(x,0),
∴42+(4﹣1)2=(x﹣4)2+42,
解得:x1=1,x2=7(舍去),
∴M(1,0),
如图3,AM=MP时,
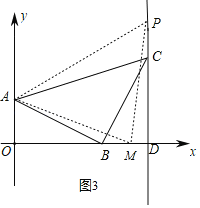
x2+12=(x﹣4)2+42,
解得x=![]() ,
,
∴![]() ,
,
综合以上可得点M的坐标为(1,0)或(![]() ).
).

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案