Question

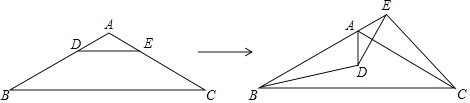
【题目】如图，在△ABC中，AB＝AC，∠B＝30°，点D、E分别为AB、AC上的点，且DE∥BC.将△ADE绕点A逆时针旋转至点B、A、E在同一条直线上，连接BD、EC.下列结论：①△ADE的旋转角为120°；②BD＝EC；③BE＝AD+AC；④DE⊥AC，其中正确的有( )

A.②③B.②③④C.①②③D.①②③④

Answer 1

【答案】B

【解析】

由AB＝AC，∠B＝30°，得出∠B＝∠C＝30°，∠BAC＝120°，得出将△ADE绕点A逆时针旋转至点B、A、E在同一条直线上，△ADE的旋转角为60°，故①错误；由DE∥BC，易证AD＝AE，得出BD＝EC，故②正确；BE＝AE+AB＝AD+AC，故③正确；证明∠DAC＝∠EAC，由AD＝AE，得出DE⊥AC，故④正确；即可得出结果.

解：∵AB＝AC，∠B＝30°，

∴∠B＝∠C＝30°，∠BAC＝120°，

∴将△ADE绕点A逆时针旋转至点B、A、E在同一条直线上，△ADE的旋转角为180°﹣120°＝60°，故①错误；

∵DE∥BC，

∴∠ADE＝∠B，∠AED＝∠C，

∴∠ADE＝∠AED，

∴AD＝AE，

∴BD＝EC，故②正确；

BE＝AE+AB＝AD+AC，故③正确；

∵∠BAC＝∠DAE＝120°，

∴∠EAC＝180°﹣∠BAC＝180°﹣120°＝60°，∠DAC＝120°﹣∠EAC＝120°﹣60°＝60°，

∴∠DAC＝∠EAC，

∵AD＝AE，

∴DE⊥AC，故④正确；

故选：B.