题目内容
【题目】如图，由12个形状、大小完全相同的小矩形组成一个大的矩形网格，小矩形的顶点称为这个矩形网格的格点，已知这个大矩形网格的宽为4，△ABC的顶点都在格点．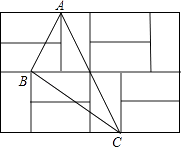
（1）求每个小矩形的长与宽；
（2）在矩形网格中找出所有的格点E，使△ABE为直角三角形；（描出相应的点，并分别用E1 ， E2…表示）
（3）求sin∠ACB的值．
【答案】
（1）
解：设每个小矩形的长为x，宽为y，
依题意得： 
，
解得 
，
所以每个小矩形的长为2，宽为1；
（2）
解：如图所示：
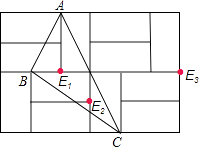
（3）
解：由图可知，S△ABC=4，设AC边上的高线为h，可知， 
ACh=4．
∵由图可计算AC=2 
，BC= 
，
∴h= 
，
∴sin∠ACB= 
= 
= 
．
【解析】（1）设每个小矩形的长为x，宽为y，根据图形可知小矩形的长与宽间的数量关系有两个：2个矩形的宽=矩形的长；两个矩形的宽+1个矩形的长=4，据此列出方程组，并解答即可；（2）利用图形和勾股定理逆定理进行解答；（3）利用面积法求得边AC上的高，然后由锐角三角函数的定义进行解答．
期末冲刺100分创新金卷完全试卷系列答案【题目】自2014年12月28日北京公交地铁调价以来，人们的出行成本发生了较大的变化. 小林根据新闻，将地铁和公交车的票价绘制成了如下两个表格。（说明：表格中“6～12公里”指的是大于6公里，小于等于12公里，其他类似）
|
| ||||||||||||||||||||||||||||||
根据以上信息回答下列问题：
小林办了一张市政交通一卡通学生卡，目前乘坐地铁没有折扣。
（1）如果小林全程乘坐地铁的里程为14公里，用他的学生卡需要刷卡交费________元；
（2）如果小林全程乘坐公交车的里程为16公里，用他的学生卡需要刷卡交________元；
（3）小林用他的学生卡乘坐一段地铁后换乘公交车，两者累计里程为12公里。已知他乘坐地铁平均每公里花费0.4元，乘坐公交车平均每公里花费0.25元，此次行程共花费4.5元。请问小林乘坐地铁和公交车的里程分别是多少公里?
